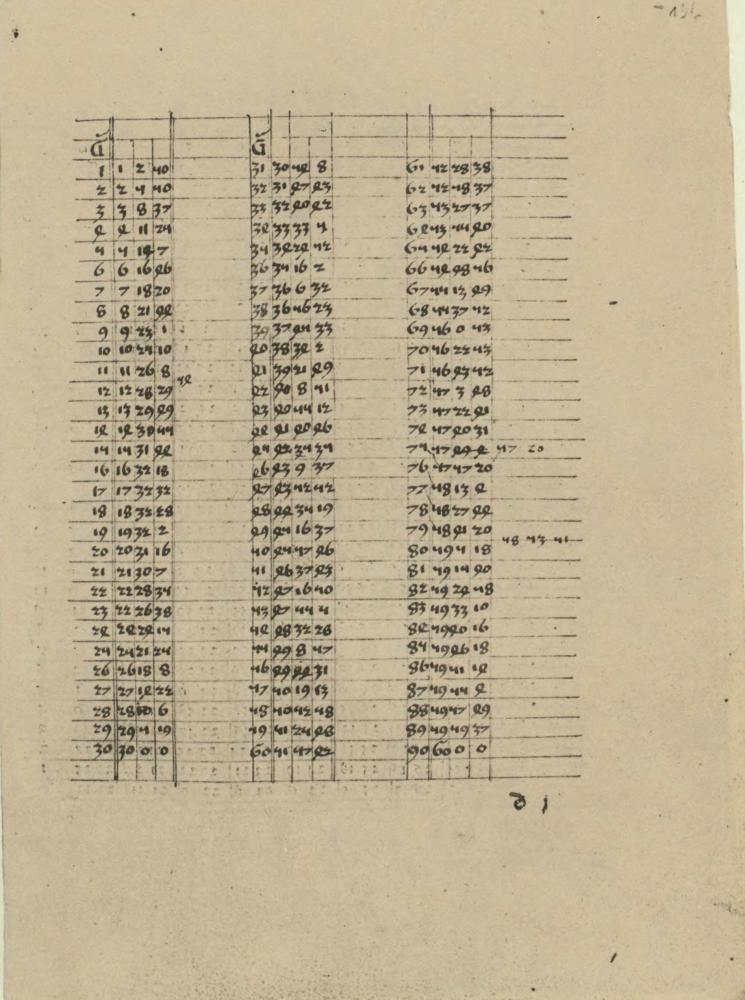
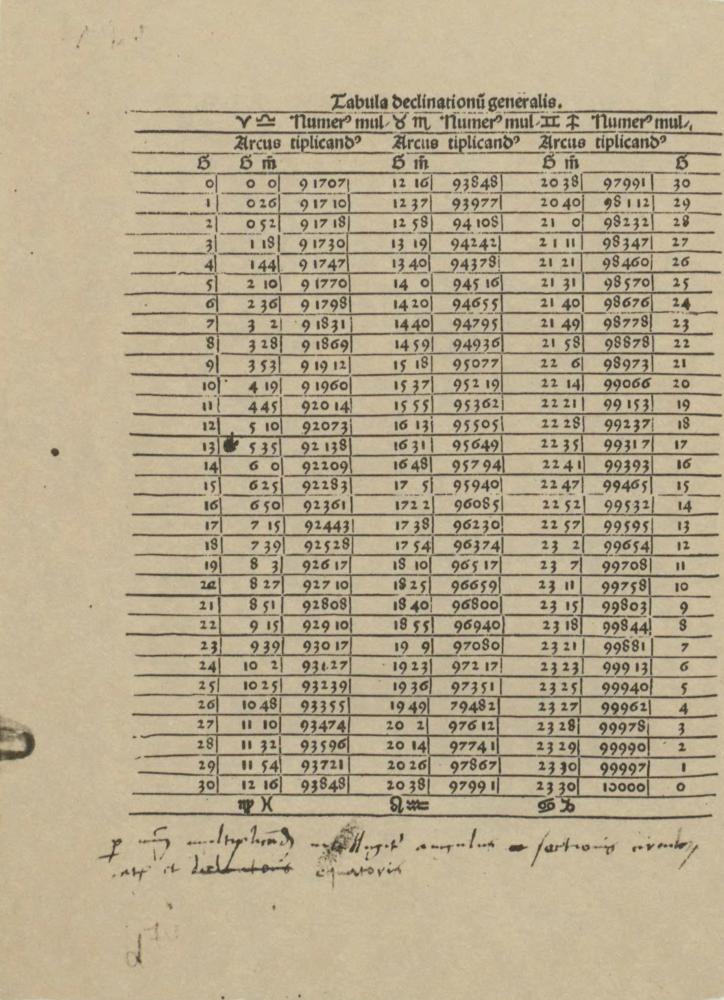
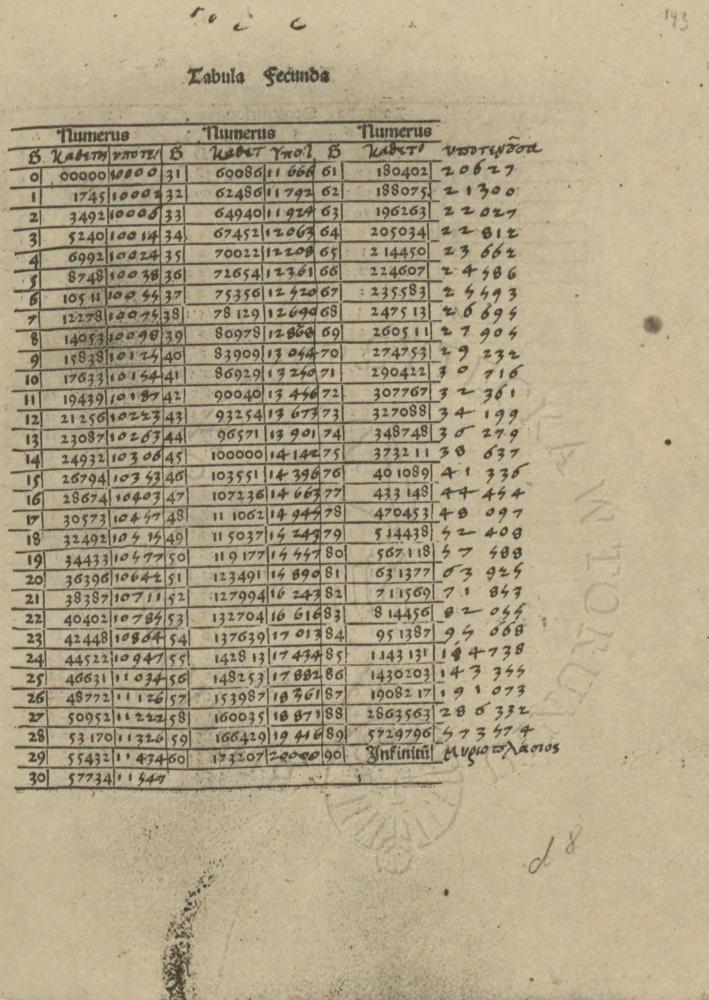
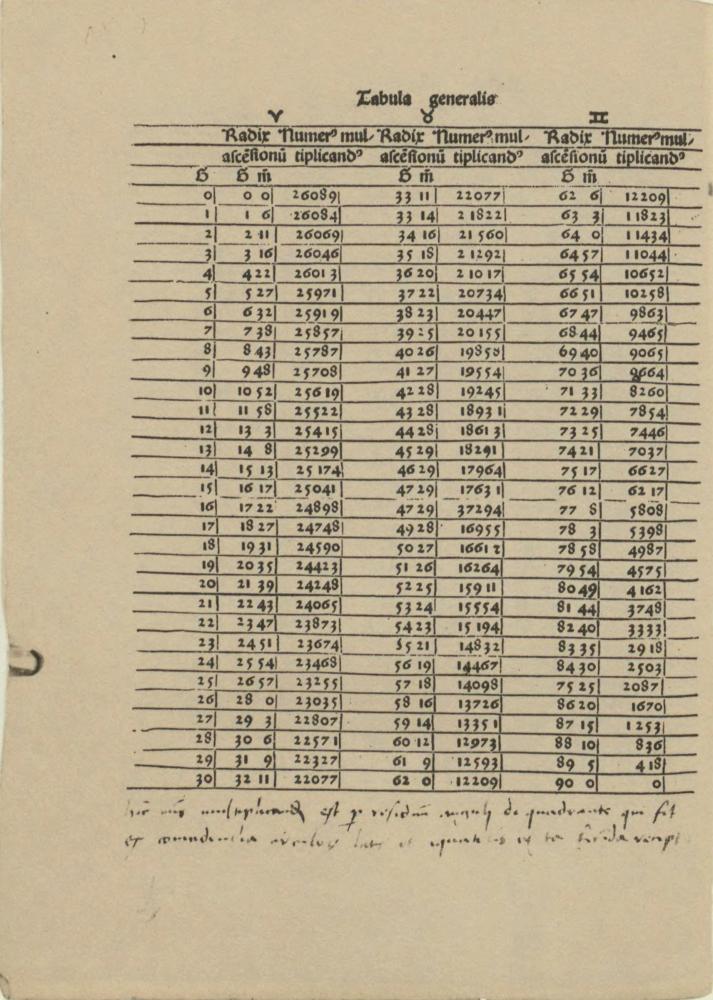
Pisma, tablice i noty astronomiczne
List Mikołaja Kopernika do Bernarda Wapowskiego, Frombork, 3 VI 1524 r.
Oryginał: zaginiony. Kopie z XVI w.: Berlin, Staatsbibliothek Preussischer Kulturbesitz, Cod. Lat. Fol. 83, k. 8–10; Wien, Österreichische Nationalbibliothek, Sammlung von Handschriften und alten Drucken, Cod. 9737, fol. 1–9v; Oxford, Bodleian Library, Ms Saville 47, fol. 28–32v.; Uppsala, Astronomska Observatoriet, Coll. Hjörter, H III. 34; Schweinfurt, Stadtarchiv, Handschrift 1 Ha 14, fol. k. 9–13 v.
Datowany z Fromborka 3 czerwca 1524 r. list Mikołaja Kopernika do Bernarda Wapowskiego w Krakowie, sekretarza królewskiego, historyka i kartografa (ok. 1445–1535), znany też jako List o ruchu ósmej sfery, nie mieści się w kategorii korespondencji bieżącej astronoma. W formalnych ramach listu zawarte jest krytyczne omówienie teorii ruchu ósmej sfery współczesnego matematyka i astronoma norymberskiego Jana Wernera.
Jan Werner z Norymbergi (1468–1522) należał do najwybitniejszych matematyków swoich czasów. Po studiach w Ingolstadt i we Włoszech żył w Norymberdze, jako wikary parafii św. Jana1. Trwałe miejsce w historii nauki zapewniły Wernerowi osiągnięcia w dziedzinie matematyki i geografii matematycznej. Był autorem trygonometrii sferycznej (wydanej z rękopisu dopiero w zeszłym stuleciu). Z osobą Wernera wiąże się wprowadzenie w matematyce metody prostaferezy (zamiana iloczynu na sumę dwóch funkcji trygonometrycznych). Do czasu wynalezienia logarytmów metoda ta stanowiła najdalej idące ułatwienie obliczeń trygonometrycznych. Trwałym śladem prac Wernera w dziedzinie kartografii jest określenie "projekcja Wernera", stosowane obecnie dla pewnego typu odwzorowania, wynalezionego prawdopodobnie w kręgu bliskich mu uczonych.
Prace Wernera ukazały się w dwóch zbiorowych tomach. W 1514 r. wydany został zbiór pism geograficznych, a w 1522 r. – już po śmierci autora – rozprawy z zakresu geometrii: In hoc opere continentur: Libellus Ioannis Werneri Nurembergensis super viginti duobus elementis conicis..., Norymberga 1522. W tomie tym znajdują się rozprawy o ruchu ósmej sfery, będące przedmiotem krytyki Kopernika: Tractatus primus de motu octavae sphaerae, qui triginta quatuor cum theorematibus tum problematibus quae propositiones libuit apellare consumatur; ...tractatus secundus in quo Alfonsinae tabulae de eodem motu ostenduntur iustis repraehensionibus non carere; Summaria enerratio theoricae motus octavae sphaere ex traditione Ioannis Werneri Nurembergensis.
Treścią rozpraw Wernera jest nowe geometryczne rozwiązanie wyjaśniające zjawiska zachodzące na skutek precesji, a więc zmianę współrzędnych (długości ekliptycznych) gwiazd oraz rozbieżność roku gwiazdowego i zwrotnikowego. Werner postuluje istnienie trzech współśrodkowych z Ziemią zewnętrznych sfer nadgwiezdnych, których ruchy, przenoszące się na sferę gwiazd stałych, powodować miały obserwowane zmiany położenia ciał niebieskich względem stałego układu odniesienia, związanego z nieruchomą Ziemią2. Kopernik miał w 1524 r. gotową koncepcję teorii precesji dzięki odkryciu "trzeciego ruchu Ziemi". Nie wspomina o niej jednak w Liście i samą teorię Wernera krytykuje bardzo zwięźle; negatywną ocenę pracy norymberskiego matematyka uzasadnia trzema argumentami dotyczącymi kwestii już bardziej szczegółowych: błędów w chronologii, pomieszania pojęć ruchu jednostajnego i średniego oraz niekonsekwentnej oceny poprawności obserwacji starożytnych.
Oryginał Listu nie zachował się, jednakże zarówno aktualność poruszanej w nim tematyki, jak i autorytet Kopernika spowodowały, że w ciągu XVI w. List był wielokrotnie odpisywany; świadectwem zainteresowania recenzją Kopernika jest aż osiem kopii Listu, zachowanych do dziś w bibliotekach europejskich. Cytował go też Tycho Brahe w wydanej w 1588 r. De mundi aetherei recentioribus phaenomenis (s. 362–363).
List został wydany drukiem po raz pierwszy w warszawskiej edycji dzieł Mikołaja Kopernika na podstawie kopii odkrytej przez W. Maciejowskiego w ówczesnej Bibliotece Królewskiej w Berlinie3. Jednocześnie z tekstem łacińskim został opublikowany polski przekład J. Baranowskiego.
Dalsze odkrywane przez badaczy odpisy z końca XVI w. oraz z XVII w. świadczą o zainteresowaniu, jakie budziło wśród astronomów europejskich pismo Kopernika. W 1875 r. I. Polkowski ogłosił wiadomość o znajdującym się w Bibliotece Polskiej w Paryżu odpisie zaginionej kopii Listu z archiwum strasburskiego4, a wkrótce M. Curtze wykorzystał odkryty przez siebie odpis z biblioteki wiedeńskiej dla opracowania krytycznej edycji5. L.A. Birkenmajerowi zawdzięczamy odkrycie dalszych kopii w Oksfordzie {Bodleian Library)6 i Uppsali (Biblioteka Obserwatorium Astronomicznego). Ta ostatnia kopia jest współoprawna z egzemplarzem bazylejskiego wydania De revolutionibus. Wreszcie w bibliotece miejskiej w Schweinfurcie odnaleziono odpis Listu pochodzący z biblioteki J. Praetoriusa7.
List do Bernarda Wapowskiego był dotychczas przekładany na język polski dwukrotnie: w warszawskim wydaniu J. Baranowskiego w 1854 r. oraz w cytowanym wyżej zbiorze kopernikanów I. Polkowskiego (przekład L. Niedźwiedzkiego z paryskiej kopii Listu).
Autorem przekładu publikowanego na portalu NICOLAUS COPERNICUS THORUNENSIS jest Jerzy Drewnowski.
Jerzy Dobrzycki
Źródło:
- Kopernik Mikołaj, Pisma pomniejsze, Warszawa 2007.
1 Z prac o Wernerze wymienić należy: S. Günther, Studien zur Geschichte der math. und phys. Geographie, Halle 1889, s. 277–332; L.A. Birkenmajer, Mikołaj Kopernik, Kraków 1900, s. 403–436; K. Schottenloher, Der Mathematiker und Astronom Johann Werner aus Nürnberg 1455–1522 [in:] Festgabe zum 7. September 1910. Hermann Grauert zur Vellendung des 60. Lebensjahres, Freiburg 1910, s. 147–155; M. Folkerts, Johannes Werner [in:] Dictionary of Scientific Biography, vol. 14, New York 1976, p. 272–277.
2 Por. J. Dobrzycki, Teoria precesji w astronomii średniowiecznej, "Studia i Materiały z Dziejów Nauki Polskiej", seria C, z. 11, 1965, s. 29–32.
3 Tekst berliński został opublikowany przez Jana Baranowskiego (Mikołaja Kopernika, Toruńczyka, O obrotach ciał niebieskich ksiąg 6, Warszawa 1854, s. 575–582). Odkryty przez Wacława Maciejowskiego, mieści się w zbiorze rękopisów z drugiej połowy XVII w., syg. Ms Lat. 83, k. 8–10. Jak wynika z adnotacji na rękopisie, tekst Listu był uprzednio dołączony do książki Kopernika, podobnie jak inne jego odpisy i odpis Zarysu.
4 Egzemplarz Biblioteki Uniwersyteckiej w Strasburgu uległ zniszczeniu w czasie wojny francusko-pruskiej w 1870 r. Zachowała się jedynie jego kopia, sporządzona w 1839 r. dla Biblioteki Polskiej w Paryżu i znajdująca się obecnie w Bibliotece Miejskiej w Strasburgu. Z końcowej zapiski w strasburskim odpisie wynika, że miał on za podstawę tekst należący do czeskiego przyrodnika Hajka i że został sporządzony w Pradze, w 1531 r. Dawniej przyjmowano (L.A Birkenmajer, Mikołaj Kopernik, Kraków 1900, s. 503–509), że chodzi tu o urodzonego w 1525 r. astronoma Tadeusza Hajka, a data 1531 – zamiast 1581 – jest jednym z wielu zresztą błędów kopisty. Być może jednak chodzi tu o Szymona Hajka, ojca astronoma, co świadczyłoby o wczesnym rozpowszechnieniu Listu znanego w Pradze już w 1531 r. (por. Z. Horsky, Bohemia and Moravia, and Copernicus, "Memoirs and Observations of Czech. Astr. Soc.", vol. 15, 1975, s. 55–56).
5 Odkryty przez M. Curtzego odpis (Biblioteka Narodowa w Wiedniu, Cod. 9737) został sporządzony, jak głosi końcowa zapiska, w 1575 r. na podstawie kopii oryginału. Wykorzystując teksty z Berlina i Wiednia Curtze opracował krytyczną edycję Listu, opublikowaną w Inedita Copernicana ("Mitteilungen d. Copp.-Ver.", Bd. l, 1878, s. 18–33).
6 Oksfordzka kopia Listu, odnotowana w osiemnastowiecznych katalogach (L.A. Birkenmajer, Mikołaj Kopernik, Kraków 1900, s. 493–497), znajduje się w Bibliotece Bodlejańskiej w kolekcji pism matematycznych i astronomicznych pochodzącej z biblioteki Henryka Saville'a (Ms. Saville 47). Ta sama biblioteka posiada dwa dalsze egzemplarze Listu, będące kopią rkps Saville 47 (Ms Smith 93 i Ms Rigaud 43). L.A. Birkenmajer odkrył w 1897 r. tekst Listu wpisany w egzemplarzu De revolutionibus (wyd. 1566 r.) w Bibliotece Obserwatorium Astronomicznego w Uppsali. List zapisany jest na kartach ochronnych i na wewnętrznej stronie tylnej tomu, zawierającego oprócz De revolutionibus, Epitome Regiomontana z 1550 r. (L.A. Birkenmajer, op.cit., l. 497–501).
7 Rękopis H 87 Biblioteki Miejskiej w Schweinfurcie pochodzi ze zbioru Jana Praetoriusa (1537–1616), ucznia Retyka, a następnie profesora matematyki w Wittenberdze.
Frombork, 3 czerwca 1524 r.
Mikołaj Kopernik pozdrawia Bernarda Wapowskiego, Wielebnego Kantora i Kanonika Katedralnego w Krakowie, Sekretarza Jego Królewskiej Mości Króla Polski, swego Wielce Czcigodnego Pana i Dobrodzieja.
Przesyłając mi przed jakimś czasem dziełko o ósmej sferze, wydane przez Jana Wernera z Norymbergi, prosiłeś mnie, najlepszy Bernardzie, żebym wyjawił Twojej Wielebności także swoje zdanie o tej pracy, którą – jak wspomniałeś – wielu zachwala. Zaiste, chętnie byłbym to uczynił, gdybym także i ja mógł ją polecić szczerze i zgodnie z prawdą, chyba że wyłącznie miałbym pochwalić pilność i wysiłek autora, zgodnie z tym, co przekazuje Arystoteles, "iż należy być wdzięcznym nie tylko tym filozofom, którzy trafnie mówili, ale również tym, którzy mówili rzeczy niesłuszne", gdyż także znajomość bezdroży niemało i nierzadko przydała się tym, co pragnęli iść po właściwej drodze. Zresztą krytyka jest mało użyteczna i nieowocna i zarozumialcem jest ten, kto woli odgrywać rolę raczej złośliwego krytyka niż twórcy. Dlatego nie chciałbym budzić gniewu ganiąc kogoś, jak długo sam nie przedstawiam czegoś lepszego. Toteż chciałbym ten przedmiot, tak jak jest, pozostawić trosce innych i przedstawić Twej Wielebności ogólnie mój pogląd. Ponieważ jednak jestem przekonany, że co innego jest złośliwie krytykować i zaczepiać, a co innego poprawiać i błędy prostować, podobnie jak pochwały różnią się od pochlebstw, nie znajduję powodu, dla którego nie miałbym zadośćuczynić Twemu życzeniu lub czemu miałoby się zdawać, że lekceważę dociekania nad tymi zagadnieniami i szczególną Twą wobec nich uwagę. Aby zaś się nie zdawało, że bezpodstawnie występuję przeciwko autorowi, postaram się wykazać jak najoczywiściej, gdzie w teorii ruchu sfery gwiazd stałych pobłądził i na czym wywód jego utyka. Być może przyczyni się to niemało do lepszego zrozumienia przedmiotu.
Najpierw więc popełnił błąd w chronologii, sądząc, że drugi rok panowania cesarza Antoninusa Piusa, w którym Klaudiusz Ptolemeusz ujął w spisie obserwowane przez siebie gwiazdy, był 150 rokiem od narodzenia Chrystusa, podczas gdy w rzeczywistości był to rok 139. Ptolemeusz stwierdza bowiem w rozdziale l księgi III swego Wielkiego układu, że rok, w którym obserwował jesienne zrównanie dnia z nocą, 463 od śmierci Aleksandra Wielkiego, był trzecim rokiem panowania Antoninusa. Od śmierci zaś Aleksandra do narodzin Chrystusa minęło lat równych egipskich 323 i 130 dni. Dla okresu od początku panowania Nabonassara do narodzenia Chrystusa przyjmuje bowiem 747 lat równych i 130 dni. Nie ma co do tego wątpliwości, a i sam autor to uznaje, jak widać z Twierdzenia XXII. Jedynie według Tablic Alfonsyńskich dodać należy jeden dzień, a to dlatego, że Ptolemeusz rachubę lat ery Nabonassara i Aleksandra Wielkiego rozpoczyna od południa pierwszego dnia pierwszego egipskiego miesiąca Thoth, Alfons zaś od południa dnia poprzedzającego, podobnie jak my liczymy lata ery Chrystusa od południa ostatniego dnia grudnia.
Według ósmego rozdziału tejże III księgi Ptolemeusza, od Nabonassara do śmierci Aleksandra Wielkiego minęły 424 lata równe. Zaświadcza to Cenzoryn w dedykowanym Kwintusowi Cerelliuszowi De die natali powołując się na Marka Warrona. Z 747 lat i 130 dni pozostają więc 323 lata i 130 dni od śmierci Aleksandra do narodzin Chrystusa, od tego zaś momentu do wspomnianej obserwacji Ptolemeusza było 139 lat równych i 303 dni. Wynika stąd, że równonoc jesienna obserwowana przez Ptolemeusza miała miejsce w roku równym 140, dziewiątego dnia miesiąca Athyr, po narodzeniu Chrystusa, czyli w 139 roku rzymskim, 25 września, w III roku Antoninusa.
Dalej, tenże Ptolemeusz w V księdze Wielkiego układu przyjmuje dla obserwacji Słońca i Księżyca, dokonanej w II roku Antoninusa, 885 lat i 203 dni od ery Nabonassara. Minęło więc od narodzenia Chrystusa 138 lat równych i 73 dni. Gdy po 14 dniach, mianowicie 9 dnia miesiąca Pharmuti, Ptolemeusz obserwował Regulusa w gwiazdozbiorze Lwa, było to 22 lutego w roku rzymskim od narodzenia Chrystusa 139, a Antoninusa roku drugim. Zdaniem autora był to rok 150. Pomylił się więc o 11 lat.
Gdyby jeszcze ktoś, nie przekonany tym, pragnął rzecz sprawdzić, to winien pamiętać, że czas jest miarą liczbową ruchów niebieskich odnoszonych do "przedtem" i "potem". Na tej bowiem podstawie określamy lata, miesiące, dni i godziny. Miara zaś i rzecz mierzona, będąc z sobą powiązane, wzajemnie się określają. Następnie, skoro tablice Ptolemeusza ułożone zostały na podstawie niedawnych jego obserwacji, to trudno przypuścić, by mogły być obarczone jakimś dostrzegalnym błędem czy niezgodnością lub, tym bardziej, by pozostawały w sprzeczności z zasadami, na których się opierają. Tak więc, jeśli ktoś przeliczy za pomocą tablic Ptolemeusza jego obserwacje Słońca i Księżyca, których położenia wyznaczone zostały w odniesieniu do Regulusa za pomocą astrolabium w II roku Antoninusa, 9 dnia miesiąca Pharmuti w pięć i pół godziny po południu, to otrzyma moment odległy od narodzenia Chrystusa nie o 149 lat, lecz o 138 lat, 88 dni i pięć i pół godziny, a od ery Nabonassara o 885 lat, 218 dni i pięć i pół godziny. Tak ujawnia się błąd, niweczący zwykle dociekania autora nad ruchem ósmej sfery, gdy mowa jest o czasie. Drugi, nie mniejszy błąd tkwi w samym założeniu, że w ciągu czterystu lat przed Ptolemeuszem gwiazdy stałe poruszane były wyłącznie ruchem jednostajnym. Aby to bliżej wyjaśnić, zwrócę uwagę, że astronomia należy do tych nauk, w których poznajemy w kolejności odmiennej od naturalnej. Na przykład naturalnym porządkiem rzeczy dopiero z faktu, że planety są bliższe Ziemi niż gwiazdy, wynika, że widoczne będą jako mniej migocące. My zaś najpierw postrzegamy, że planety nie iskrzą się, i dzięki temu poznajemy, że są bliższe Ziemi. Podobnie najpierw stwierdzamy, że ruchy ciał niebieskich wydają się niejednostajne, a następnie wnosimy o istnieniu epicykli, kół mimośrodowych i innych, które taki właśnie ruch nadają. Pragnę więc powiedzieć, że starożytni uczeni musieli najpierw z pomocą przyrządów wyznaczyć położenie planet i przedziały czasu, i z tą jakby wskazówką – aby nie pozostał nierozwiązany problem ruchów ciał niebieskich – wynaleźć teorię, którą mogli uważać za ustaloną, gdy przyjęte w niej i obserwowane położenia planet zgadzały się z sobą całkowicie. Tak również ma się rzecz z ruchem ósmej sfery, którego, wobec nadmiernej jego powolności, nie mogli w pełni wyjaśnić. Chcąc badać ten ruch, trzeba jednak iść ich śladem i trzymać się ich obserwacji pozostawionych nam jakby w testamencie. Jeśliby ktoś, zadufany we własnym rozumie, uważał, że nie należy im wierzyć, to na pewno brama naszej nauki pozostanie dla niego zamknięta i leżąc przed wejściem śnić będzie chorobliwe urojenia o ruchu ósmej sfery. Zasługuje też na to, zwłaszcza swoim mniemaniem, że oczerniając starożytnych wspomoże własne halucynacje. Wiadomo przecież, że starożytni, którzy pozostawili nam wiele świetnych i podziwu godnych odkryć, przeprowadzali obserwacje z najwyższą starannością i biegłością. Nikt więc nie przekona mnie, jakoby mogli mylić się w wyznaczaniu położeń gwiazd o jedną czwartą, jedną piątą lub choćby jedną szóstą stopnia, jak przypuszcza autor i o czym będzie jeszcze mowa niżej.
Nie można również pomijać, że przy każdym ruchu niebieskim, obarczonym zmiennością, należy przede wszystkim dążyć do wyznaczenia pełnego okresu, w którym ruch przejdzie przez wszystkie swe nierówności.
Dostrzegana nierówność ruchu powoduje bowiem, że z niepełnego obiegu nie można wyznaczyć całego okresu i średniej prędkości. Jak jednak Ptolemeusz, a przed nim Hipparch stwierdzili z wielką przenikliwością przy badaniu ruchu Księżyca, w ruchu zmiennym występują cztery momenty, w przeciwległych punktach okręgu, a mianowicie największej i najmniejszej szybkości oraz na prostopadłej średnicy – szybkości średniej; dzielą one koło na cztery części tak, że w pierwszej ćwiartce maleje najszybszy ruch, w drugiej maleje średni, a w trzeciej wzrasta ruch najwolniejszy i w czwartej średni. W ten sposób, obserwując i badając ruch Księżyca mogli stwierdzić, w której części okręgu znajduje się on w dowolnym czasie, a stąd, gdy powracała ta sama szybkość ruchu poznawali, że minął pełny okres nierówności, jak to wyjaśnił obszernie Ptolemeusz w IV księdze Wielkiego układu. Należałoby tego przestrzegać również przy badaniu ruchu ósmej sfery. Jego nadmierna powolność, o której już mówiłem, że po tysiącach lat nie powtórzyła się jeszcze ta sama nierówność biegu, nie pozwala ustalić od razu całości okresu, przekraczającego życie wielu pokoleń. Można to jednak osiągnąć czyniąc rozsądne przypuszczenia i wykorzystując niektóre obserwacje z czasów po Ptolemeuszu, odpowiadające powyższym zasadom. Co bowiem zostało wyznaczone, nie pozwala na dowolność w wyjaśnieniu, podobnie jak wykreśliwszy koło przez trzy punkty nie leżące na prostej nie można przez nie wykreślić innego, większego lub mniejszego. O tym jednak przy innej okazji i wracam do tematu, od którego zboczyłem.
Zobaczmy więc, czy rację ma autor twierdząc, że gwiazdy stałe w ciągu 400 lat przed Ptolemeuszem zmieniały swe położenie jedynie ruchem równym. Aby nie pomylić się co do znaczenia wyrazów, określam ruch równy, który zwykliśmy również nazywać średnim, jako pośredni między najszybszym i najwolniejszym. Niech nas nie zmyli, co pisze autor w pierwszym Dopełnieniu do Twierdzenia VII, że "ruch gwiazd był wolniejszy", skoro według jego teorii był równy, a później szybszy, a więc nigdy nie mógł być wolniejszy. Nie wiem, czy pozostaje w zgodzie sam z sobą mówiąc później o ruchu znacznie wolniejszym. Oparł zaś miarę ruchu średniego na jednostajności ruchu gwiazd, wynoszącym od czasów pierwszych obserwatorów Timocharisa i Arystarcha do Ptolemeusza około jednego stopnia na stulecie, co już dostatecznie wykazał Ptolemeusz, a powtórzył autor w Twierdzeniu szóstym. Jednakże, wielkim okazując się matematykiem, nie spostrzegł, że w pobliżu punktów równości, to jest przecięć ekliptyki dziesiątej sfery i – jak je nazywa – kół trepidacji, ruch gwiazd żadną miarą nie może wydawać się bardziej jednostajny niż gdzie indziej. Przeciwnie, musi wtedy okazać się najbardziej zmienny, najmniej zaś, gdy jest najszybszy lub najwolniejszy. Autor winien był to zauważyć bądź z własnych założeń i systemu, bądź z tablic na nich opartych, zwłaszcza z ostatniej, obejmującej pełny okres nierówności, czyli trepidacji. Według tej tablicy w dwóch stuleciach przed narodzeniem Chrystusa, zgodnie z poprzednim obliczeniem, dostrzegany ruch wyniósł w ciągu pierwszych 100 lat tylko 49', w drugim stuleciu 57'. Następnie po narodzeniu Chrystusa w ciągu pierwszego wieku przemieściły się gwiazdy stałe o jeden i około jednej dziesiątej stopnia, w drugim stuleciu o prawie jeden i jedną czwartą stopnia, tak że ruch w jednakowych okresach różni się o nieco mniej niż jedną szóstą stopnia. Jeśli zaś dodać ruch w obu dwustuletnich okresach, to w pierwszym do dwóch stopni brakuje ponad jedną piątą, w drugim przekracza je prawie o około jedną czwartą. Tak więc ruch w późniejszym z tych dwóch rocznych okresów jest szybszy o około jedną drugą i jedną piętnastą stopnia od ruchu w okresie wcześniejszym, gdy uprzednio autor, dając wiarę Ptolemeuszowi, przyznawał gwiazdom ruch jednego stopnia na stulecie.
Z drugiej strony z tych samych założeń autora co do kręgów wynika, że przy najszybszym ruchu ósmej sfery w ciągu 400 lat występuje różnica zaledwie jednej minuty w dostrzeganym ruchu, co widać we wspomnianej tablicy, na przykład dla okresu od 600 do 1000 roku po Chrystusie. Podobnie jest przy ruchu najwolniejszym, w ciągu 400 lat od roku 2060.
Regułą w ruchu niejednostajnym jest, jak już powiedziano wyżej, że w jednym półkolu trepidacji, a mianowicie od najmniejszej do największej szybkości, stale wzrasta dostrzegana szybkość, w drugim natomiast półkolu, od ruchu najszybszego do najwolniejszego, stale maleje, a przyspieszenie i zwalnianie największe jest w przeciwległych punktach ruchu średniego. Tak więc widome ruchy w dwóch następujących po sobie okresach mogą być równe tylko w pobliżu położeń odpowiadających największej lub najmniejszej szybkości. Wokół tych punktów wyrównuje się ruch zaczynający lub kończący przyspieszanie względnie zwalnianie.
Żadną miarą więc nie mógł być średni ów ruch w ciągu 400 lat przed Ptolemeuszem, a raczej najwolniejszy. Nie mamy podstaw do przypuszczenia, by kiedyś był jeszcze powolniejszy, skoro nie zachowała się ani do naszych czasów, ani nawet do czasów Ptolemeusza, żadna obserwacja gwiazd sprzed epoki Timocharisa. I skoro ruch najszybszy już minął, jesteśmy w innym niż Ptolemeusz półkolu nierówności. Z półkola tego, w którym szybkość maleje, niemała już część została przebyta.
Nie może przeto dziwić, że autor opierając się na tych swoich założeniach nie mógł głębiej wniknąć w obserwacje starożytnych i sądził, że mylili się oni o jedną czwartą lub jedną piątą, a nawet o połowę i więcej stopnia. A przecież Ptolemeusz nigdzie nie wykazał większej pilności jak w staraniu, aby przekazać nam poprawny opis ruchu gwiazd stałych, przekonany, że nie może sobie pozwolić na żaden błąd w odniesieniu do tej małej części, na podstawie której odtwarza całość owego obiegu. Najmniejsza bowiem pomyłka mogła nadmiernie zaważyć wobec bardzo długiego okresu tego ruchu. Dlatego zestawia aleksandryjczyka Timocharisa z współczesnym mu Arystarchem oraz Menelaosa rzymianina z Agryppą z Bitynii, aby dzięki ich – mimo oddalenia – zgodności uzyskać prawdziwe i pewne dowody. Jeszcze mniej prawdopodobne jest więc, by tak wielkie błędy popełniali czy to oni, czy też Ptolemeusz, którzy potrafili dużo trudniejsze nawet kwestie wyjaśniać do najdrobniejszego szczegółu.
Nigdzie wreszcie nie okazał się bardziej niedorzeczny jak w Twierdzeniu XXII, a zwłaszcza w Dopełnieniu, gdy zalecając własne dzieło, gani Timocharisa z powodu dwóch gwiazd, a mianowicie Kłosa i północnej z trzech na czole Niedźwiadka. Twierdząc, że obliczenie daje za małą wartość dla pierwszej, za dużą zaś dla drugiej, zbyt dziecinnie tutaj majaczy. Przesunięcie gwiazd między obserwacjami Timocharisa i Ptolemeusza wynosi bowiem cztery stopnie i trzecią część, wartość prawie równą dla obu gwiazd wobec równego niemal odstępu czasu. Autor nie zauważył, że 4° 7' dodane do miejsca gwiazdy, ustalonego przez Timocharisa jako 2° Niedźwiadka, nie może dać 6°40' Niedźwiadka, gdzie obserwował ją Ptolemeusz, i – na odwrót – odjęcie tej samej wielkości od 26°40' Panny, podanej przez Ptolemeusza, nie mogło doprowadzić do poprawnej wartości 22°20', a tylko do 22°32'. Tak oto uważał, że rachunek o tyle daje tutaj za mało, jak tam za dużo, jak gdyby rozbieżność tkwiła w obserwacjach lub jakby droga z Aten do Teb nie była ta sama co z Teb do Aten. Zresztą gdyby w obu przypadkach liczbę dodał lub odjął tak, jak tego wymaga identyczność rozumowania, stwierdziłby zgodność wyników. Dodaj jeszcze, że – jak mówiłem na początku – między Timocharisem i Ptolemeuszem były nie 443, lecz tylko 432 lata. Tak więc krótszemu okresowi odpowiada mniejsza wartość i autor rozminie się z obserwowanym ruchem gwiazd już nie o 13', ale o jedną trzecią stopnia. W ten sposób własny błąd przypisał Timocharisowi, ledwo pobłażając Ptolemeuszowi. Lecz gdy twierdzi, że ich wyznaczeniom nie można ufać, to co pozostaje, jak nie ufać i jego obserwacjom?
Tyle o ruchu ósmej sfery w długości. Możesz stąd łatwo wywnioskować, co sądzić należy o ruchu deklinacji. Ująć go w dwóch, jak je określa, trepidacjach, nakładając jedną na drugą. Lecz skoro zburzony już został sam fundament, upaść musi budowa słaba i sprzeczna. Co wreszcie sam sądzę o ruchu sfery gwiazd stałych? Ponieważ inne na to przeznaczam miejsce, przeto za zbyteczne i niewłaściwe uważam dłużej się tu rozwodzić. Wystarczy bowiem, jeżeli dostatecznie spełniłem Twoje życzenie, wypowiadając, jak żądałeś, me zdanie o tym dziełku. Życzę jak najlepszego zdrowia Twej Wielebności.
We Fromborku, 3 czerwca 1524.
Mikołaj Kopernik
Przekład Jerzego Drewnowskiego
Frombork, 3 czerwca 1524 r.
Reuerendo domino Bernhardo Vapouski, Cantori et Canonico Ecclesiae Cracouiensis et S. R. Maiestatis Poloniae etc. Secretario, Domino et Fautori suo plurimum Obseruando, S. D. Nicolaus Copernicus Cum pridem ad me mitteres, optime Bernharde, Iohannis Werneri Nurembergensis editum De motu octauae sphaerae opusculum, quod a multis laudari dicebas, petijt ex me Venerabilitas tua, vt ei meam quoque sententiam de illo significarem. Quod certe tamo libentius fecissem, quanto honestius et re vera a me quoque commendari potuisset, nisi quod studium hominis et conatum laudem, et quod admonuit Aristoteles: "Non solum ijs, qui bene locuti sum, gratificandum esse philosophis, sed etiam non recte locutis". Quandoquidem non parum saepe contulit etiam deuia notassse viam rectam sequi volentibus. Caeterum ad modicum vtilis est reprehensio confertque parum, quin et impudentis ingenij est Momum potius agere velle quam poetam. Proinde etiam vereor, ne mihi succenseat aliquis, si alium reprehendam, quamdiu ipse non profero meliora. Itaque volebam illa, vt sum, dimittere curae aliorum, atque sic Venerabilitati tuae vt mentem meam acciperet, in summa responsum fuisse. Verum cum animaduertam aliud esse mordere et lacessere quemquam, aliud castigare et reuocare errantem, quemadmodum vicissim laudare aliud est quam adulari et agere parasitum, non inuenio, cur desiderio tuo obsequi non deberem, quod harum rerum studio et diligentia, qua praecipue polles, derogare viderer. Ac proinde, ne etiam emere videar reprehendere hominem, conabor quam apertissime ostendere, in quibus ille de motu sphaerae stellarum fixarum errauerit neque conueniat eius traditio. Quod forsitan ad certiorem eius rei capessendam rationem non parum etiam conducet.
Primum igitur fefellit illum supputatio temporum, quod existimauerit annum secundum Antonini Pij Augusti, quo Claudius Ptolemaeus obseruata a se fixa sydera in ordinem constituit, fuisse a natiuitate Christi anno CL cum fuerit secundum veritatem annus CXXXIX. Ptolemaeus enim libro tertio Magnae Constructionis, capite primo, obseruatum autumni aequinoctium ab Alexandri Magni morte anno CCCCLXIII ait fuisse Antonini anno tertio, a morte vero Alexandri ad Christi natiuitatem numerantur anni pariles Aegyptij CCCXXIII et CXXX dies. Nam a principio regni Nabonassaris ad Christi natiuitatem supputant annos pariles DCCXLVII et dies CXXX, de quo non video dubitari neque autorem hunc, vt apparet propositione XXII, nisi quod additur dies vnus secundum Canones Alphonsinos. Idque ideo, quod Ptolemaeus incipit a meridie primi diei primi mensis Thot bo apud Aegyptios annos Nabonassarios et Alexandri Magni, Alphonsus autem a meridie vltimi diei anni praecedentis, quemadmodum nos a meridie vltimi diei mensis Decembris annos Christi supputamus. A Nabonassare autem ad excessum Alexandri Magni Ptolemaeus eodem libro capite octauo numerat bt annos CCCCXXIIII pariles. Cui adstipulatur Censorinus De die natali ad Quintum Cerelium scribens, autoritate Marci Varronis. Relinquuntur ergo ex annis DCCXLVII et CXXX diebus CCCXXIII anni et CCXXX dies, videlicet ab Alexandri morte ad Christi natiuitatem. Atque hinc ad Ptolemaei obseruationem iam dictam anni pariles CXXXIX et dies CCCIII. Ergo obseruatum a Ptolemaeo aequinoctium hoc autumni constat fuisse a natiuitate Christi annorum parilium CXL, nona die mensis Athyr, Romanorum vero annorum CXXXIX, die XXV Septembris, Antonini tertio.
Rursus idem Ptolemaeus libro quinto Magnae Constructionis, capite tertio, in obseruatione Solis et Lunae anno secundo Antonini supputat annos Nabonassarios DCCCLXXXV et CCCIII dies. Fuissent ergo a Christi natiuitate anni transacti pariles CXXXVIII et LXXIII dies. Exinde post dies XIV, nempe Pharmuti nono, quo Ptolemaeus Leonis Basiliscum obseruauit, erat a natiuitate Christi Romanorum annus CXXXIX, XXII dies Februarij. Atque hic Antonini annus secundus, quem putat autor iste CL fuisse. Fefellit igitur se ipsum supra annos XI.
Adhuc autem si quis dubitet et his non contentus cupiat etiam huius rei capere experimentum, meminisse debet tempus esse numerum siue mensuram motus coeli secundum prius et posterius. Hinc enim anni, menses, dies et horae nobis constant. Mensura autem et mensum vicissim se habent, relatiua sunt enim. Porro Canones Ptolemaei cum essent adhuc ex recenter a se obseruatis conditi, credibile non est errorem aliquem ab his sensu perceptibilem vel discrepantiam continere, quominus suis principijs, quibus incumbunt, non congruerent. Quae cum ita sint, si loca Solis et Lunae circa Basiliscum organis astrolabicis inuenta a Ptolemaeo anno secundo Antonini, nouem diebus Pharmuti mensis quinque horis et dimidia a meridie transactis per tabulas ipsius inquirendo numeret, non inueniet ea post annos Christi CXLIX, sed post CXXXVIII annos, LXXXVIII dies et horas quinque et dimidiam. Qui sunt Nabonassaris DCCCLXXXV anni, dies CCXVIII et horae quinque et dimidia. Ita iam error iste manifestus est, qui illius inquisitionem de motu octauae sphaerae plerumque infecit ubi temporum facit mentionem.
Alius error est non minor praecedenti in ipsa eius hypothesi, in qua existimat CCCC annis ante Ptolemaeum aequali tantummodo motu non errantia sydera mutata fuisse. Quae vt apertius (quae inferius) dicentur, magisque perspicua fiant, animaduertendum puto scientiam stellarum eorum esse, quaecunque praepostere cognoscuntur a nobis, quam secundum naturam. Quemadmodum, verbi gratia, prius natura nouit viciniores esse Terrae planetas quam fixa sydera: deinde quod sequitur, vt minus vibrantes appareant. Nobis e contrario antea visi sunt planetae non scintillare et exinde cognitum propinquiores esse Terrae. Ita pariformiter prius deprehensum est anobis inaequales videri stellarum motus. Postea epicyclia esse, eccentros aliosue circulos, quibus ita ferantur, ratiocinamur. Atque ideo dictum id esse velim, quod oportuerit priscos illos philosophos primum loca stellarum instrumentorum artificio notare, tum temporum interuallis et ea tamquam manuductione quadam, (ne infinita quaestio de motu caeli remaneret) rationem aliquam de eis certam percunctari, quam tunc visi sunt inuenisse, quando consideratis visisque stellarum locis adstipulatione quadam omnibus conueniret. Ita etiam de motu octauae sphaerae se habet, quem prisci mathematici ob nimiam eius tarditatem nobis ad plenum tradere non potuerunt. Sed vestigia eorum sequenda sunt inuestigare eum volentibus et eorum considerationibus tanquam testamento relictis inhaerendum. Quod si quis suo sensui inhaerens putauerit illis non concedendum in hoc, certe huic clausa est ianua huius artis et ante ostium recubans aegrotantium somnia de motu octauae sphaerae somniabit. Et merito, vtputa qui per illorum calumniam existimauerit suae hallucinationi subueniendum. Constat autem illos summa diligentia et solerti ingenio omnia obseruasse, qui multa et praeclara inuenta et admiratione digna nobis reliquerunt. Quamobrem persuadere mihi haudquaquam possum in accipiendis stellarum locis eos errasse vel in quarta vel quinta siue etiam sexta parte vnius gradus, vt hic autor existimat, de quo postea latius.
Illud quoque praetereundum non est in omni motu sydereo cui diuersitas inest, totam reuolutionem ante omnia desiderari, in qua intelligatur omnes motus apparentes differentias pertransiuisse. Diuersitas enim apparens in motu est, quae impedit, vt per partes tota reuolutio et aequalitas motus mensurari non possit. Sed sicut in inquisitione cursus Lunaris Ptolemaeus et ante eum Hipparchus Rhodius magna ingenij sagacitate considerauerunt, oportet esse quatuor momenta in reuolutione diuersitatis opposita sibi inuicem per diametros, vtputa extremae velocitatis et tarditatis, ac vtrobique per transuersum ambarum aequalitatum mediantium quadrifariam secantia circulum, fitque, vt in primo quadrante velocissimus decrescat motus, in altero diminuatur medius, et rursus crescat tardissimus in tertio quadrante, aequalis in quarto. Qua industria scire potuerunt ex obseruatis inspectisque Lunae motibus, in qua circuli portione quolibet tempore verteretur. Ac proinde, cum similis motus redijsset, intellexerunt iam factam inaequalitatis circuitio- nem lh . Quemadmodum hoc latius Magnae Constructionis libro quarto Ptolemaeus explicauit.
Quod etiam in inquisitione motus octauae sphaerae erat obseruandum. Sed nimia eius, vt dixi, tarditas (qua in annorum milibus nondum in sese reuersus inaequalitatis motus satis constat) non sinit id statim absoluere, quia multas hominum aetates excedit. Possibile tamen est coniectura rationabili ad id perueniri posse adiutos etiamnum aliquibus obseruationibus post Ptolemaeum adauctis, quae in eandem congruerint rationem. Nam quae determinata sunt, infinitam rationem habere non possunt. Quemadmodum, si per tria puncta non secundum rectam lineam posita circumferentia ducatur, non licet aliam superinducere, quae maior vel minor fuerit prius transmissae. Sed de his alias, vt reuertar ad id, vnde digressus sum.
Videndum igitur nobis nunc est, an recte se habeat quod dicit non errantia sydera CCCC ante Ptolemaeum annis aequali solummodo motu fuisse mutata. Porro, ne verborum significatione fallamur, aequalem accipio motum, quem et mediocrem dicere solemus, qui sit inter tardissimum et concitatissimum medius. Ne circumueniat nos, quod in corollario primo septimae propositionis dicit "tardiorem esse motum fixorum syderum", vbi penes suam hypothesin aequalem ponit, caeterum velociorem: perinde ac si nunquam futurus sit tardior. In quibus haud scio, an sibi ipsi constet, multo tardiorem postea adducens. Asseruit autem aequalitatis argumentum ex vniformitate, qua fixa sydera tantisper a primis stellarum fixarum obseruatoribus, Aristarcho et Timochare, vsque ad Ptolemaeum, ac per aequalia temporum interualla, vtputa per singulos annorum centenarios, singulos proxime gradus pertransiuerint. Vt apud Ptolemaeum satis apparet repetitum ab autore propositione septima.
Sed hic tantus mathematicus existens non aduertit, quod nullatenus esse potest, vt circa momenta aequalitatis, hoc est sectiones circulorum eclipticae decimae sphaerae et trepidationis, vt ille vocat, vniformior appareat stellarum motus quam alibi, quando contrarium eius sequi necesse sit, vt tunc maxime varius appareat, minime vero, quando velocissimus vel tardissimus est motus apparens. Quod vel e sua ipsius hypothesi et constructione debebat animaduertere et tabulis inde contextis, praesertim vltimo Canone, quem ad reuolutionem totius inaequalitatis siue trepidationis exemplificauit. Vbi a CC annis ante natiuitatem Christi secundum praecedentem supputationem in primo annorum centenario reperitur motus apparens scrupulorum primorum XLIX duntaxat vnius gradus; in altero centenario scrupulorum primorum LVII. Deinde ab ipsa natiuitate Christi per primum annorum centenarium transmutatae fuissent stellae gradu vno et decima fere parte vnius; in secundoi gradu vno et quarta fere, vt paulo minus sextante vnius gradus se inuicem excedant motus sub aequalibus temporum spacijs. Quod si coniungas CC annorum vtrobique motum, deficiet in primo interuallo a duobus gradibus plus quam quinta pars vnius. In secundo autem superaddet prope vnius quadrantem, sicque rursus sub aequalibus temporibus excedet motus sequens praecedentem in dimidio gradu et parte quintadecima fere, cum antea centesimo quoque anno singulos pertransisse im gradus stellas fixas Ptolemaeo credens detulisset. E contrario vero eadem lege assumptorum a se circulorum in velocissimo motu octauae sphaerae contingit, vt in CCCC annis vix vnius scrupuli differentia in motu apparente reperiatur. Quemadmodum videre licet ab annis Christi DC vsque ad M in eodem Canone. Similiter et in tardissimo, vt a MMLX annis in subsequentes CCCC. Et ratio diuersitatis est, quia, vt dictum est superius, in vno hemicyclio trepidationis (a summa videlicet tarditate ad summam velocitatem) accrescit semper aliquid motui apparenti ac in altero semicirculo (qui a summa velocitate ad tarditatem) continuo decrescit motus, qui antea creuerat, fitque summa augmentatio et diminutio in punctis aequalitatis e diametro oppositis. Adeo vt in motu apparente non sit reperirei motus aequales in duobus continuis temporum spacijsi, qui alter altero maior fiat aut minor, nisi circa velocitatis aut tarditatis extremitates, vbi duntaxat vltro citroque aequales circumferentiae pertranseunt temporis aequalitate atque incipientes vel desinentes augeri vel minui mutua tunc sese compensatione coaequant.
Nulla ergo ratione conuenit medium fuisse motum eum, qui in CCCC annis ante Ptolemaeum, sed tardissimum potius. Cum etiam non videam, cur alium diuinemur tardiorem, de quo nullam coniecturam hactenus habere potuimus, cum ante Timocharem nulIa stellarum fixarum annotatio facta sit, quae ad nos vsque peruenisset, sed neque ad Ptolemaeum. Cumque velocissimus etiam motus iam praeterierit, consequens est in altero a Ptolemaeo semicirculo iam nos esse, in quo diminuitur motus, cuius etiam non modica pars praeterierit.
Itaque mirum videri non debet, quod non potuerit hisce suis assumptionibus propius accedere ad ea, quae sunt ab antiquis annotata, putaueritque illos aberrasse in quarta vel quinta parte vnius gradus, siue etiamnum dimidia et amplius: cum tamen in nulIa parte Ptolemaeus maiorem videatur adhibuisse diligentiam, quam vt nobis non errantium stellarum motum sine vitio traderet, attendens, quod non nisi in modica eius particula id sibi fuisset concessum, qua in vniuersum illum circuitum coniecturus esset. Vbi error quantumlibet insensibilis interueniens in tota illa vastitate insignis nimirum poterat euenire. Ideoque Timochari Alexandrino Aristarchum adiunxisse videtur coaetaneum et Menelao Romano Agrippam Bythinium, vt sic etiam in tanta locorum distantia illis consentientibus verissima haberet et indubitata testimonia, quominus credibile sit eos vel Ptolemaeum in tanto errasse, qui multa alia etiam it difficiliora ad extremum, vt aiunt, vnguem deprehendere potuerunt.
NulIo demum loco ineptior est quam in XXII propositione et praesertim corollario eiusdem, dum opus hoc suum commendare volens taxat Timocharem circa duas stellas , vtputa Aristam Virginis et eam, quae ex tribus in fronte Scorpij borealior est, quod supputatio eius in illa deficiat, in hac autem abunder: vbi nimis pueriliter hallucinatur. Cum enim sit eadem vtriusque stellae distantia inter Timocharem et Ptolemaeum consideratarum, nempe gradus IV et tertia pars sub aequali fere temporis differentia, atque numerus supputationis illius perinde idem proxime, nihilo tamen magis aduertit, quod gradus IV, scrupula VII addita loco stellae, quam reperit Timochares in secundo gradu Scorpij, merito non possent supplere VI gradus et scrupula XX Scorpij, vbi Ptolemaeus ipsam inuenit. Et e conuerso idem numerus eleuatus ex XXVI gradibus et XL scrupulis Aristae secundum Ptolemaeum vsque ad gradum XXII et tertiam partem redire, vt par est, non potuit, sed residebat in XXII gradibus et scrupulis XXXII. Ita existimabat illic defecisse calculum, quanto hic abundasset, tanquam in obseruationibus haec incidisset diuersitas, vel quasi ex Athenis in Thebas et e Thebis in Athenas eadem via non sit. Alioqui si vtrobique vel addidisset numerum vel subduxisser, vt paritas rationis postulabat, inuenisset vtrumque eodem modo sese habere.
Adde etiam, quod reuera non erant inter Timocharem et Ptolemaeum anni CCCCXLIII, sed CCCCXXXII solum, vt a principio declaraui. Proinde breuiori tempore minorem esse numerum oportet, vt non solum in scrupulis XIII, sed in triente vnius gradus ab obseruato stellarum motu dissidebat. Ita errorem hunc suum imposuit Timochari vix euadente Ptolemaeo. At dum existimat illorum annotationibus non fidendum, quid aliud restat, quam vt suis quoque obseruationibus minus credatur?
Et haec de in longitudinem motu octauae sphaerae. E quibus etiam facile potest intelligi, quid de motu quoque declinationis existimandum sit. Inuoluit enim ipsam duabus, vt ait, trepidationibus inserendo secundam hanc supra primam. Sed dissipato ipso iam fundamento necesse est, vt superaedificata corruant infirmaque sint, ac minus sibi inuicem cohaerentis. Quid demum ipse de motu non errantium stellarum sphaerae semiam, quoniam alio loco destimata sum, superfluum putaui et impertinens hic amplius immorari, cum satis sit, si modo desiderio tuo satisfecerim, vt meam, quod a me exigebas, de isto opusculo habeas sententiam. Valeat Venerabilitas tua quam faustissime.
Ex Varmia 3 Iunij Anno MDXXIV
Nicolaus Copernicus
Zarys podstaw astronomii, znany pod łacińskim tytułem Commentariolus
Oryginał: zaginiony
Commentariolus to najważniejsze, pochodzące z początków XVI w., przedstawienie teorii heliocentrycznej, której wpływ miał ważne znaczenie dla nowych modeli astronomii jeszcze w następnym stuleciu1. Radykalne poparcie dla astronomii heliocentrycznej, choć bez powoływania się imiennie na źródła, przedstawiał i opublikował w 1640 r. matematyk i astronom, profesor Wojciech Strażyc2, w rozprawie pod tytułem Questio astronomica in Alma Academia Cracoviensi, jako temat do publicznej debaty. Także na uniwersytecie w Rostocku jeszcze w połowie XVII w. odbył się cykl seminariów poświęcony Kopernikowskiemu porządkowi świata3.
W krótkim, zwięzłym wykładzie Kopernik podał w Zarysie nowe rozwiązania geometryczne i podstawowe wartości niektórych parametrów ruchu planet. Zakres treściowy i forma wykładu pozwalają na wskazanie bezpośredniego wzoru literackiego w tak zwanych teorykach planet, należących do podstawowego kanonu pism astronomicznych europejskiego późnego średniowiecza. Proweniencja teoryk sięga starożytności; od połowy XV w. naczelne miejsce zajęły Nowe teoryki planet Jerzego Peurbacha (wykładane i komentowane w Krakowie w okresie studiów Kopernika). Umieszczając Zarys w tej tradycji piśmienniczej podkreślić trzeba konsekwentne przeciwstawianie przez Kopernika tez dotyczących podstawowego układu odniesienia (heliocentrycznego) tezom Nowych teoryk planet Peurbacha (układu geocentrycznego)4. Teoria precesji omawiana przez Peurbacha (jako "ruch ósmej sfery") na końcu teoryk, w Zarysie została umieszczona przed teorią Księżyca i planet. W podobny sposób różnił się układ treści Obrotów – głównego dzieła Kopernika i Almagestu Ptolemeusza.
W Zarysie Kopernik zapowiedział opublikowanie pełnego wywodu o charakterze matematycznym w późniejszym "większym dziele". Jednakże astronomia heliocentryczna w Obrotach nie była prostym rozwinięciem założeń podanych w Zarysie. Różnice między obu dziełami dotyczą przede wszystkim modeli orbit planetarnych: w Zarysie są one dwuepicykliczne, przy czym pierwszy epicykl wraz z deferentem odpowiadają mimośrodowym deferentom planet, jakie przyjmował Kopernik dla planet w Obrotach. Dalsze zmiany dotyczyły teorii precesji, w Zarysie zaledwie naszkicowanej. Po napisaniu Zarysu nastąpiło też odkrycie przez Kopernika ruchomości linii absyd planetarnych, dokonane dzięki porównaniu obserwacji własnych ze starożytnymi. Do własnych ustaleń odwołuje się Kopernik tylko w jednym fragmencie Zarysu, przy określaniu długości roku gwiazdowego; poza tym wykorzystuje dane liczbowe przyjmowane powszechnie we współczesnej mu astronomii, czerpane przede wszystkim z Tablic astronomicznych króla Alfonsa i ze skróconej wersji łacińskiej Almagestu Ptolemeusza, opracowanej przez Jerzego Peurbacha i Jana Regiomontana (Epitome in Almagestum, Wenecja 1496).
Jakie było przeznaczenie Zarysu? Krytykując w Liście do Bernarda Wapowskiego teorię ruchu ósmej sfery Jana Wernera, Kopernik powstrzymał się od przedstawienia własnych poglądów. Jeszcze w ostatnich latach życia, pisząc List dedykacyjny do Obrotów, wspominał o swej niechęci do rozpowszechniania wiadomości o nowej teorii. Fakty te świadczą, że Zarys również nie był przeznaczony dla dużej liczby czytelników, lecz jedynie dla osób z bliskiego mu kręgu. Owego szczupłego grona odbiorców Zarysu szukać trzeba przede wszystkim w środowisku naukowym Krakowa, z którym Kopernik utrzymywał wieloletnie kontakty. Bezpośrednim tego dowodem jest wzmianka o "rozprawie głoszącej, że Ziemia się porusza, a Słońce pozostaje nieruchome" w inwentarzu biblioteki Macieja z Miechowa z 1514 r.5
Data powstania Zarysu była przedmiotem wielu studiów; może być jednak ustalona jedynie w przybliżeniu. Odkrywca Zarysu M. Curtze mylnie uważał go za krótkie wprowadzenie do Obrotów. L.A. Birkenmajer zwrócił pierwszy uwagę na istotne różnice w szczegółach teorii w Zarysie i w Obrotach oraz wskazał na przesłanki dla ustalenia okresu, w którym Zarys musiał być napisany. Widoczna w tekście Zarysu znajomość Epitome Regiomontana i Peurbacha, wydanego w Wenecji w 1496 r., oraz Almanachu z 1502 r. pozwala na stwierdzenie, że Zarys pisany był po tej ostatniej dacie. Z kolei cytowana wyżej wzmianka w inwentarzu z 1514 r. zdaje się świadczyć, że traktat Kopernika dotarł do Krakowa – a więc oczywiście i był napisany przed 1514 r. Późniejszą datę napisania Zarysu wykluczyć można również wobec faktu, że bezpośrednio po tej dacie podjął Kopernik prace teoretyczne i obserwacyjne, które doprowadziły do wspomnianych już zmian w geometrycznych szczegółach teorii. Węzłowe znaczenie dla datowania Zarysu ma wzmianka Marcina Raabego (Korwina) w wierszu zamieszczonym na wstępie kopernikowskiego przekładu Listów Teofilakta Symokatty, opublikowanego w Krakowie w 1509 r. W wierszu tym Korwin sławi Kopernika, stwierdzając, że "zjawisk przyczyny on na podziwu godnych umie objaśniać zasadach"6. Owe "podziwu godne zasady" można zapewne wiązać z istnieniem sformułowanego już zarysu nowej teorii astronomicznej. Pismo Kopernika powstałoby więc najprawdopodobniej około 1509 r.
Autograf Zarysu nie zachował się, a uratowanie jego tekstu w odpisach zawdzięczać należy w dużej mierze Tychonowi Brahemu. Otrzymawszy w 1575 r. kopię Zarysu od czeskiego astronoma Tadeusza Hajka, Tycho Brahe rozpowszechniał rozprawę Kopernika w odpisach wśród współczesnych astronomów. Relacja o tym, zawarta w Astronomiae instauratae progymnasmata7, pozostawała przez następne stulecia jedynym drukowanym świadectwem istnienia Zarysu.
W 1878 r. Curtze8 opublikował tekst Zarysu na podstawie kopii, odkrytej w ówczesnej Cesarskiej Bibliotece Dworskiej w Wiedniu (dziś Austriacka Biblioteka Narodowa). Wiedeński odpis jest niekompletny, brak w nim mianowicie jednej karty zawierającej większą część rozdziału omawiającego teorię ruchu Księżyca. Pochodził z kręgu Tychona Brahego i należał do jego asystenta, duńskiego astronoma Christiana Sørensena Longomontanusa9.
Trzy lata później, w 1881 r., odkryty został przez A. Lindhagena drugi, tym razem kompletny, odpis Zarysu w bibliotece Królewskiej Akademii Nauk w Sztokholmie10. Tekst jest zapisany na kartach współoprawnych z egzemplarzem drugiego wydania Obrotów (Bazylea 1566), pochodzącym z biblioteki Jana Heweliusza. Na podstawie obu przekazów L. Prowe opracował krytyczne wydanie tekstu, opublikowane w 1884 r.11 Wydanie to było jednak obarczone pomyłkami i niepoprawionym błędami samych przekazów; do ich usunięcia przyczynili się wydawcy przekładów, w niewielkiej mierze niemieckich12, a przede wszystkim autorzy komentowanych przekładów angielskich, E. Rosen i N. Swerdlow13. Nową wersję oryginalnego tekstu łacińskiego, na podstawie obu wspomnianych już przekazów, opracował w 1953 r. R. Gansiniec.
Odkryty w latach sześćdziesiątych ubiegłego stulecia trzeci odpis Zarysu, znajdujący się w Bibliotece King's College w Aberdeen14, jest kopią z 1585 r., sporządzoną w Rostocku przez Duncana Liddela i zapisaną na interfoliach bazylejskiego wydania Obrotów z 1566 r. Jej podstawą był zapewne tekst Tychona Brahego, pozostającego w tym okresie w kontaktach naukowych z Liddelem15.
Tłumaczenie Jerzego Drewnowskiego, zamieszczone na portalu NICOLAUS COPERNICUS THORUNENSIS, jest pierwszym polskim przekładem całego dziełka i ma za podstawę tekst łaciński przygotowany do trzeciego tomu Opera omnia Nicolai Copernici według wszystkich trzech przekazów: z Wiednia, Sztokholmu i Aberdeen. W opracowaniu wykorzystano wspomnianą wyżej wersję recenzji Zarysu, pochodzącą ze spuścizny po zmarłym w 1958 r. prof. Ryszardzie Gansińcu, opartą na odpisach wiedeńskim i sztokholmskim. Z recenzji tej przejęto w szczególności interpunkcję i ortografię.
Jerzy Dobrzycki
Źródło:
- Kopernik Mikołaj, Pisma pomniejsze, Warszawa 2007.
1 J. Kepler, Epitome astronomiae Copernicanae, Linz 1621, rozdz. 7.
2 Treść i znaczenie wykładów Strażyca zostały przedstawione w: J. Dobrzycki, Święty Jerzy gra na skrzypkach, czyli krakowski spór o podstawy i metody nauki w XVII wieku, "Odrodzenie i Reformacja w Polsce", t. 42, 1998, s. 75–81.
3 De Systemate Mundi Copernicano, Discursus Physico Mathematicus, In Illustri Academia Rostochiensi, Sex Disputationibus Publicis Propositus, Rostock 1652.
4 J. Dobrzycki, Notes on Copernicus’s Early Heliocentrism, "Journal for the History of Astronomy", vol. 32, 2001, s. 223–225.
5 Opublikowana przez L.A. Birkenmajera w: Stromata Copernicana, Kraków 1924, s. 200–202.
6 Teofilakt Symokatta, Listy, tłum. J. Parandowski, Warszawa 1953, s. 132.
7 Tycho Brahe, Astronomiae instauratae progymnasmata, Praga 1602, patrz Tychonis Brahe Dani Opera omnia, vol. II, s. 428.
8 "Mittheilungen des Coppernicus-Vereins", Bd. l, 1878, s. 1–17.
9 Austriacka Biblioteka Narodowa w Wiedniu, rkps 10530, k. 34–43 (w dawnej numeracji k. 56–59,61–66).
10 Tekst Zarysu pochodzi zapewne z przełomu XVI i XVII w., zapisany jest ręką na ośmiu kartach współoprawnych z egzemplarzem drugiego wydania De revolutionibus Kopernika w Bibliotece Królewskiej Akademii Nauk w Sztokholmie. Są to karty 2–9 poszytu liczącego łącznie 39 kart, poza tekstem Zarysu, pustych. Papier nosi znak wodny "orzeł z pastorałem na piersi" (Briquet, t. I, nr 1357), odpowiadający dacie produkcji około 1580 r. Wydanie: A. Lindhagen, "Bihang till K. Svenska Vet. Akad. Handlingar", 6, 1880-1882, nr 12 (1881), s. 1–15; reprodukcja rękopisu: M. Kopernik, Dzieła wszystkie, t. 4, tabl. LV.
11 L. Prowe, Nicolaus Coppernicus, Bd. 2, Berlin 1884, s. 184–202.
12 A. Müller w "Zeitschrift für Geschichte und Altertumskunde Ermlands", Bd. 12, 1899, s. 359–382; F. Rossmann, Nicolaus Kopemicus, Erster Entwurf seines Weltsystems, Monachium 1948.
13 E. Rosen, Three Copemican Treatises, 3 wyd., Nowy Jork 1971; N. Swerdlow, The Derivation and First Draft of Copernicus's Planetary Theory, "Proceedings of the American Philosophical Society", vol. 117, 1973, s. 423–512.
14 W.P.D. Wightman, Science and the Renaissance, vol. 2. Edynburg 1962, s. 67; J. Dobrzycki, W.P.D. Wightman, The Commentariolus of Copernicus, "Nature", vol. 208, 1965, s. 1263; J. Dobrzycki, The Aberdeen copy of Copernicus's Commentariolus, , "Journal for the History of Astronomy”, t.4, 1973, s. 124–127.
15 Duncan Liddell (1551–1613), szkocki lekarz i astronom, sporządził odpis Zarysu w Rostocku w listopadzie 1585 r. Treść traktatu Kopernika jest rozrzucona na kartach papieru współoprawnych z drugim wydaniem De revolutionibus: wstęp – przed k. 1 (początek I księgi); teoria ruchu Słońca i punktów równonocy przed k. 86 (przy rozdz. 15, księgi III); Księżyc przed k. 101 (ks. IV, rozdz. 3); planety górne przed k. 149 (ks. V, rozdz. 9); Wenus przed k. 161 (ks. V, rozdz. 20) i Merkury przed k. 169 (ks. V, rozdz. 29). Według relacji Tychona Brahego (De nova stella, Frankfurt 1610, s. 479) duński astronom otrzymał traktat Kopernika w 1575 r. od Tadeusza Hajka i przekazał go "alijs quibusdam in Germania mathematicis". Reprodukcja rękopisu: M. Kopernik, Dzieła wszystkie, t. 4, tabl. LIV.
(CZĘŚĆ WSTĘPNA)
Wielką liczbę sfer niebieskich przodkowie nasi przyjęli, jak sądzę, dla zachowania regularności w pozornym ruchu planet. Całkowicie niedorzeczne wydawało się bowiem przypuszczenie, że ruch ciała niebieskiego, odbywający się w doskonałej kolistości, może być niejednostajny. Zauważyli zaś, że wskutek złożenia się i połączenia dwóch ruchów regularnych może się wydawać, iż coś porusza się do jakiegoś miejsca niejednakowo.
Kallippos i Eudoksos starali się to wyjaśnić teorią kół współśrodkowych. Nie potrafili jednak wytłumaczyć przy jej pomocy wszystkich zjawisk ruchu planet. Nie wyjaśnili ani ich pozornych ruchów, ani tego, że raz wydaje się nam, iż planety oddalają się, innym zaś razem, że się przybliżają, co nie da się pogodzić z zasadą współśrodkowości. Dlatego słuszniejsze wydało się mniemanie, iż dzieje się tak dzięki kołom mimośrodowym i epicyklom. Pogląd ten przyjęła w końcu większość uczonych. Jednakże to, co głosili Ptolemeusz i wielu innych, pozostawało wprawdzie w zgodzie z danymi liczbowymi, ale budziło również niemałe wątpliwości. Tłumaczenia te nie były bowiem wystarczające bez dodatkowego wprowadzenia pewnych fikcyjnych kół wyrównujących, z których wynikało, że planeta ani na swojej sferze unoszącej, ani w odniesieniu do środka swego epicykla nie porusza się z zawsze jednakową prędkością. Toteż tego rodzaju system nie wydawał się ani dostatecznie doskonały, ani wystarczająco zgodny z rozumem.
Zauważywszy te braki, często się zastanawiałem, czy by się nie dało wynaleźć racjonalniejszego układu kół, od których zależałyby wszelkie pozorne nierówności ruchów i które obracałyby się ruchem jednostajnym względem własnych środków tak, jak tego wymaga zasada ruchu doskonałego.
Przystąpiwszy do tego trudnego i niemal nierozwiązywalnego problemu, znalazłem wreszcie sposób, w jaki można tego dokonać przy pomocy kół o wiele mniej licznych i o wiele bardziej ze sobą zgodnych, niż przyjmowano dawniej, jeśli tylko wolno nam będzie przyjąć następujące założenia, zwane aksjomatami.
Założenie pierwsze
Nie istnieje jeden środek wszystkich sfer niebieskich.
Założenie drugie
Środek Ziemi nie jest środkiem świata, lecz tylko środkiem ciężkości i sfery Księżyca.
Założenie trzecie
Wszystkie sfery krążą wokół Słońca jako środka i dlatego w pobliżu Słońca znajduje się środek świata.
Założenie czwarte
Stosunek odległości Słońca od Ziemi do wysokości firmamentu jest o tyle mniejszy od stosunku promienia ziemskiego do odległości Słońca, że odległość ta jest niezauważalna w porównaniu z wielkością firmamentu.
Założenie piąte
Każdy ruch widoczny na firmamencie jest wywołany nie jego własnym ruchem, lecz ruchem Ziemi. Ziemia więc, wraz z otaczającymi ją żywiołami, w ciągu doby obraca się cała w swoich niezmiennych biegunach, podczas gdy firmament i najwyższe niebo pozostają nieruchome.
Założenie szóste
Cokolwiek spostrzegamy jako ruch Słońca, nie jest jego własnym ruchem, lecz skutkiem ruchu Ziemi i naszej sfery, z którą się obracamy wokół Słońca podobnie jak każda inna planeta; Ziemia wykonuje zatem kilka ruchów.
Założenie siódme
To, co u planet wydaje się ruchem wstecznym lub posuwaniem się naprzód, nie pochodzi od nich, lecz od Ziemi. Jej więc ruch sam wystarczy dla wyjaśnienia tak wielu nierówności dostrzeganych na niebie.
Po przedstawieniu tych założeń spróbuję pokrótce wykazać, z jaką konsekwencją da się utrzymać jednostajność ruchów. Sądzę, że dla zwięzłości należy tu pominąć dowody matematyczne przeznaczone do większego dzieła. Objaśniając koła, podamy tu jednak wielkości promieni sfer, dzięki czemu człowiek biegły w matematyce z łatwością pojmie, jak dobrze taki układ zgadza się z liczbami i obserwacjami.
Aby zaś nikt nie sądził, że ruchomość Ziemi przyjmujemy za Pitagorejczykami zbyt pochopnie, także i tutaj podamy przekonywający dowód objaśniając koła. Główne bowiem argumenty, którymi filozofowie przyrody starają się udowodnić nieruchomość Ziemi, po większej części oparte są na zjawiskach i wszystkie zostaną tu od razu obalone, gdy wyjdziemy poza pozory.
O kolejności sfer
Sfery niebieskie zamykają się w sobie w następującej kolejności. Najwyżej znajduje się nieruchoma, wszystko zawierająca i mieszcząca sfera gwiazd stałych. Po niej następują kolejno sfery Jowisza, Saturna i Marsa, a pod tą ostatnią mamy sferę, na której my jesteśmy unoszeni. Pod nią zaś znajduje się sfera Wenus i wreszcie ostatnia z nich - sfera Merkurego*. Sfera Księżyca obraca się wokół środka Ziemi i z nim razem unosi się niby epicykl. W tej kolejności jedna sfera przewyższa drugą prędkością obrotu w zależności od rozmiarów ich kół. Saturn wraca do położenia wyjściowego po trzydziestu latach, Jowisz - po dwunastu, Mars - po dwóch, Ziemia - po rocznym obrocie, Wenus po dziewięciu miesiącach, Merkury - po trzech.
* Tłumacz niezgodnie z oryginałem wskazał kolejność sfer planet. Treść tłumaczenia odpowiadająca oryginałowi: "Sfery niebieskie są ułożone w następującej kolejności. Najwyższa z gwiazd stałych jest nieruchoma i zawiera w sobie i umieszcza wszystko, poniżej niej znajduje się Saturn, następnie Jowisz, a następnie Mars. Poniżej znajduje się sfera, w której się obracamy, następnie Wenus, a na końcu Merkury".
O POZORNYCH RUCHACH SŁOŃCA
Ziemia podlega trzem ruchom. Pierwszym jest ruch na wielkim kole, z którym okrążając Słońce według kolejności znaków zodiaku dokonuje obrotu w ciągu roku, zakreślając w jednakowych odstępach czasu zawsze jednakowe łuki; środek tego kręgu oddalony jest od środka Słońca o dwudziestą piątą część swego promienia. Promień ten, jak sądzimy, ma wielkość niedostrzegalną w porównaniu z wielkością firmamentu. Dlatego wydaje się, że Słońce porusza się po kole takim ruchem, jakby Ziemia leżała w środku świata. Tymczasem dzieje się to nie wskutek ruchu Słońca, lecz Ziemi.
Kiedy na przykład znajduje się ona w znaku Koziorożca, Słońce widoczne jest na wprost, w kierunku średnicy, w znaku Raka i tak dalej. Ponadto wskutek wspomnianej odległości Słońca od środka koła będzie się wydawało, że wykonuje ono ten ruch niejednostajnie; największe odchylenie powstające z tej przyczyny wynosi dwa i jedną szóstą stopnia. Punkt firmamentu, ku któremu Słońce oddala się od środka, leży w odległości prawie 10 stopni na zachód od bardziej błyszczącej spośród dwóch gwiazd, znajdujących się na głowie jednego z Bliźniąt. Wtedy więc Słońce jest widoczne w największej odległości, kiedy Ziemia znajduje się naprzeciw, a środek sfery leży między nimi. Po tym kole krąży nie tylko Ziemia, lecz także wszystko, co jest zamknięte razem ze sferą Księżyca.
Innym ruchem Ziemi, szczególnie jej właściwym, jest codzienny obrót w biegunach według kolejności znaków, to jest w kierunku wschodnim. Skutkiem tego ruchu jest wrażenie, że cały świat obraca się z zawrotną szybkością. W ten sposób obraca się Ziemia z otaczającą wodą i sąsiednim powietrzem.
Trzecim ruchem jest ruch deklinacji. Oś codziennego obrotu nie jest bowiem równoległa do osi wielkiego koła, lecz nachyla się do niej o taką część obwodu, która w naszych czasach wynosi prawie 23 i pół stopnia. Tak więc środek Ziemi pozostaje zawsze w płaszczyźnie ekliptyki, tzn. na obwodzie wielkiego koła, a bieguny jej krążą, zakreślając po obu stronach małe kręgi wokół środków jednakowo odległych od osi wielkiego koła. Również ten ruch dokonuje się w okresie prawie rocznym i jest niemal równy obrotowi wielkiego koła. Natomiast oś wielkiego koła nie zmienia swego położenia względem firmamentu, lecz przechodzi zawsze przez te same jego punkty, zwane biegunami ekliptyki. Podobnie ruch deklinacji połączony z ruchem koła skierowywałby bieguny codziennego obrotu zawsze ku tym samym miejscom na niebie, gdyby okresy tych obydwu obrotów równały się sobie całkowicie. Obecnie po upływie długiego przeciągu czasu stwierdzono, że położenie Ziemi względem firmamentu ulega zmianom. To spostrzeżenie skłoniło większość do przyjęcia opinii, że sam firmament wykonuje jakieś ruchy na mocy prawa niedostatecznie jeszcze znanego. O wiele mniej zaskakujące jest jednak wyjaśnienie, że wszystko to może być skutkiem ruchomości Ziemi. Nie do mnie natomiast należy odpowiedź na pytanie, ku czemu bieguny się skierowują. W rzeczach podrzędniejszych znane mi jest podobne zjawisko, przejawiające się tym, że pręcik żelazny potarty magnesem zwraca się zawsze ku jednemu miejscu świata. Słuszniejszy wszakże wydaje się pogląd, że położenie biegunów zależy od jakiejś sfery, która swym zmieniającym się nachyleniem wprawia je w ruch. Sfera ta niewątpliwie powinna się znajdować poniżej Księżyca.
Jednostajność ruchów należy odnosić nie do punktów równonocnych, lecz do gwiazd stałych.
Ponieważ punkty równonocne i pozostałe główne punkty świata zmieniają swe położenie w znacznym stopniu, musi się mylić każdy, kto stara się z nich wyprowadzić stałą długość obrotu rocznego. Na podstawie wielkiej liczby obserwacji w różnych czasach przyjmowano różne jej wartości. Hipparch określił ją na 365 dni, 5 godzin i 46 minut, a więc że jest o 13 i trzy piąte minuty […], czyli o jedną trzecią minuty krótszy niż ustalony przez Ptolemeusza. Hispalensis natomiast sądził, że długość ta jest o dwudziestą część godziny większa od przyjętej przez Albategniego, ustalił bowiem, że rok zwrotnikowy równa się 365 dniom, 5 godzinom i 49 minutom.
Nie należy jednak sądzić, że różnice pochodzą tu z błędów obserwacji. Dokładniejsze zbadanie szczegółów prowadzi bowiem do stwierdzenia, że te różne wartości liczbowe po- zostają zawsze w zgodzie z przesuwaniem się punktów równonocnych. Albowiem wtedy, kiedy te główne punkty świata przesuwały się tylko o jeden stopień w ciągu stu lat, jak to stwierdzono w czasach Ptolemeusza, długość roku pozostawała taka, jaką przekazał sam Ptolemeusz. Kiedy zaś w następnych stuleciach poruszały się z większą szybkością, wychodząc naprzeciw ruchom odbywającym się niżej, rok stał się o tyle krótszy, o ile przesunięcie się głównych punktów było większe. Szybciej bowiem biegnąc w przeciwnym kierunku, w krótszym czasie spotykały się z ruchem rocznym. Słusznie więc uczyni ten, kto równość roku odniesie do gwiazd stałych. Postępując w ten właśnie sposób posłużyłem się Kłosem Panny i obliczyłem, że długość roku wynosi 365 dni i prawie sześć i jedną szóstą godziny, tak jak przyjmowano również w starożytnym Egipcie. Tę samą metodę należy stosować także w odniesieniu do innych ruchów planet, o czym pouczają ich absydy, ustalone prawa ruchów na firmamencie i prawdziwe świadectwo samego nieba.
O KSIĘŻYCU
Księżyc, oprócz wspomnianego już obiegu rocznego, wykonuje jeszcze cztery ruchy. Mianowicie na swoim kole unoszącym, czyli deferencie, obraca się w ciągu miesiąca wokół środka Ziemi zgodnie z kolejnością znaków. Na deferencie tym unosi się epicykl, zwany zwykle epicyklem pierwszej nierówności lub epicyklem argumentu, a który my będziemy nazywali pierwszym albo większym. Ten większy epicykl w czasie niewiele dłuższym od miesiąca wykonuje obrót, który w górnej jego części odbywa się w kierunku przeciwnym do ruchu deferentu. Do niego z kolei jest przymocowany mniejszy epicykl, na którym dopiero znajduje się Księżyc wykonujący w ciągu miesiąca dwa obroty w kierunku przeciwnym do ruchu epicykla większego. Ilekroć środek większego epicykla dotknie linii przechodzącej od środka wielkiego koła przez środek Ziemi (którą to linię nazywamy promieniem wielkiego koła), tylekroć Księżyc będzie się znajdował najbliżej środka większego epicykla, co następuje w czasie nowiu i pełni. Natomiast najbardziej oddalony od tego punktu będzie w kwadrach, czyli w połowie drogi między nowiem i pełnią. Promień zaś większego epicykla stanowi dziesiątą część promienia swego deferentu i jedną osiemnastą tejże dziesiątej części i równy jest jednocześnie pięciokrotności mniejszego epicykla bez jego czwartej części.
Wynikiem tego układu jest wrażenie, że Księżyc raz jest szybszy, raz wolniejszy, że zbliża się i oddala, a ruch mniejszego epicykla do tej pierwszej nierówności dodaje jeszcze dwie nieregularności, mianowicie odciąga Księżyc od jednostajności ruchu po obwodzie większego epicykla; powstająca w ten sposób nieregularność osiąga 12 i jedną czwartą stopnia okręgu o odpowiedniej wielkości, czyli promieniu; ponadto skutkiem tego ruchu środek większego epicykla raz oddala się od Księżyca, raz się do niego przybliża o wielkość promienia epicykla mniejszego. Ponieważ z tej przyczyny Księżyc zakreśla wokół środka większego koła różnej wielkości, pierwsza nierówność znacznie się zmienia. Dlatego w czasie koniunkcji ze Słońcem i w czasie opozycji do niego nie przekracza 4 stopni i 56 minut, podczas gdy w kwadrach zwiększa się do 7 stopni i 36 minut. Ci zaś, którzy tłumaczą to kołem mimośrodowym, przyjmują niestosowną niejednostajność jego ruchu, a poza tym popadają w dwa oczywiste błędy. Z obliczeń matematycznych wynika bowiem, że Księżyc w kwadrach, kiedy znajduje się na najniższej części epicykla, wydawałby się prawie czterokrotnie większy (jeśliby tylko błyszczał cały) niż w nowiu i w pełni, chyba że ktoś przyjmie nierozsądnie, iż objętość Księżyca wzrasta i maleje. Także paralaksa Księżyca powinna zwiększać się znacznie w kwadrach, ponieważ wielkość Ziemi w porównaniu z jej odległością od Księżyca jest już znacząca. Jednakże jeśli ktoś zbada tę sprawę dokładniej, stwierdzi, że obie te wartości są niemal takie same w kwadrach jak podczas nowiu oraz pełni, i nie będzie miał wątpliwości, że nasze wyjaśnienie jest prawdziwsze.
Wykonując te trzy ruchy w długości, Księżyc przechodzi przez punkty swego ruchu w szerokości. Osie epicykli są równoległe do osi deferentu i dlatego Księżyc pozostaje zawsze w jego płaszczyźnie. Natomiast oś deferentu odchyla się od osi wielkiego koła, czyli ekliptyki, skutkiem czego Księżyc oddala się od płaszczyzny ekliptyki. To zaś odchylenie równa się 5 stopniom obwodu koła. Bieguny deferentu krążą w jednakowej odległości od osi ekliptyki, prawie tak samo jak w omówionej już deklinacji. I w tym wypadku następuje to w kierunku odwrotnym do kolejności znaków zodiaku, lecz o wiele wolniej, tak że jeden obrót dokonuje się w ciągu dziewiętnastu lat. Większość sądzi, że dzieje się to w wyżej położonej sferze, do której są przyczepione bieguny deferentu poruszające się w ten właśnie sposób. Taki jest, jak się wydaje, mechanizm ruchów Księżyca.
O TRZECH PLANETACH GÓRNYCH: SATURNIE, JOWISZU I MARSIE
Saturn, Jowisz i Mars mają podobną zasadę ruchów, albowiem ich sfery, zamykając w sobie całkowicie wielkie koło roczne, obracają się w kierunku zgodnym z kolejnością znaków wokół środka tego koła, który jest również ich wspólnym środkiem. Lecz deferent Saturna wykonuje pełny obrót w ciągu trzydziestu lat, Jowisza - w ciągu dwunastu, Marsa zaś - 29 miesięcy, tak jakby wielkość orbit wpływała hamująco na prędkość obrotów. jeśli bowiem promień wielkiego koła podzielimy na 25 części, promień deferentu Marsa będzie miał 38 takich części, Jowisza - 130 i pięć dwunastych, Saturna - 230 i jedną szóstą. "Promieniem deferentu" nazywam odległość od środka koła do środka pierwszego epicykla. Każdy bowiem z tych deferentów ma dwa epicykle, z których jeden unosi się na drugim, podobnie jak to przedstawiono w związku z Księżycem, lecz według innych prawideł.
Pierwszy epicykl poruszając się w kierunku przeciwnym do ruchu deferentu wykonuje w danym czasie tę samą co on liczbę obrotów. Drugi zaś, który unosi planetę, obraca się w kierunku przeciwnym do ruchu pierwszego z prędkością dwukrotnie większą. Skutkiem tego, kiedy znajdzie się w największej odległości od środka deferentu, albo na odwrót - w najbliższym jego sąsiedztwie, wtedy planeta będzie najbliżej środka pierwszego epicykla; kiedy natomiast ten drugi epicykl znajdzie się w odległości ćwiartki koła, czyli w połowie drogi między tymi miejscami, wtedy będzie najbardziej oddalona od tegoż środka. Wskutek połączenia takich ruchów deferentu i epicykli oraz w wyniku jednakowej prędkości ich obrotów, tego rodzaju punkty największego i najmniejszego oddalenia zajmują stałe miejsce na firmamencie. Z tejże przyczyny planety w każdym miejscu zachowują niezmienne prawidła ruchu i absydy mają w stałych miejscach: Saturn koło gwiazdy, o której mówią, że znajduje się nad łokciem Strzelca, Jowisz - 8 stopni za gwiazdą, zwaną końcem ogona Lwa, Mars zaś - 6 i pół stopnia przed sercem Lwa.
Wielkości epicykli są następujące. Jeśli wielkie koło podzielimy tak jak przedtem na 25 części, to promień pierwszego epicykla Saturna będzie się składał z 19 takich części i 41 minut, promień drugiego będzie ich miał 6 i 34 minuty. Pierwszy epicykl Jowisza będzie miał promień równy 10 częściom i 6 minutom, drugi - 3 i 22 minutom. Promień pierwszego epicykla Marsa będzie miał 5 części i 34 minuty, drugiego l część i 51 minut. Tak więc w każdym wypadku promień większego epicykla jest trzykrotnie większy od promienia mniejszego.
Nierówność, którą ruch epicykli wprowadza do ruchu planety po deferencie, nazwiemy nierównością pierwszą. Jak już powiedziano, zachowuje ona w każdym miejscu firmamentu stałe wartości. Jest jeszcze druga nierówność, która przejawia się w tym, że planeta niekiedy zdaje się cofać, a często także przystawać, co nie jest wynikiem jej własnego ruchu, lecz zmieniającego się położenia Ziemi. Albowiem, jeśli popatrzeć na planetę na tle firmamentu, wobec szybszego ruchu Ziemi ruch planety będzie ustępować. To cofanie się jest najbardziej widoczne wtedy, kiedy Ziemia znajduje się najbliżej planety, to znaczy kiedy wchodzi w środek między Słońce i planetę w okresie jej wieczornego wschodu. Przeciwnie zaś w okresie, kiedy planeta zachodzi wieczorem lub wschodzi rano, Ziemia poruszając się szybciej przyspiesza widoczny jej ruch. Wtedy zaś, kiedy planeta, jak ją oglądamy na niebie, przesuwa się w kierunku przeciwnym do swego rzeczywistego ruchu z tą samą prędkością, wskutek wzajemnego znoszenia się ruchów powstaje wrażenie, że planeta się zatrzymuje. Ma to miejsce wtedy, kiedy odległość między planetą a Słońcem jest bokiem trójkąta równobocznego (Ziemia, Słońce, planeta). U wszystkich tych planet nierówność tego rodzaju jest tym większa, im niżej znajduje się deferent, po którym planeta się porusza. Dlatego mniejsza jest u Saturna niż u Jowisza, a znowu największa u Marsa, według stosunku promienia wielkiego koła do promieni ich deferentów. U każdej planety jest ona największa wtedy, gdy linia wzroku biegnąca w kierunku planety jest styczna do obwodu wielkiego koła. W ten sposób poruszają się te trzy planety.
W szerokości zaś odchylają się dwojako. Ponieważ obwody ich epicykli znajdują się w tej samej płaszczyźnie co ich deferenty, odchylają się od płaszczyzny ekliptyki według nachyleń swych osi. Osie te jednak nie obracają się, tak jak w wypadku Księżyca, lecz zwracają się zawsze w tę samą stronę nieba. Dlatego punkty przecięcia się kół deferentu i ekliptyki, zwane węzłami, zajmują na firmamencie wiecznie te same miejsca. I tak Saturn swój węzeł, w którym zaczyna się wznosić w kierunku północnym, ma 8 i pół stopnia za gwiazdą, którą nazywają gwiazdą na głowie wschodniego z Bliźniąt, Jowisz - 4 stopnie za tą samą gwiazdą, a Mars 6 i pół stopnia przed Hiadami. Planeta, znajdując się w tych punktach albo diametralnie im przeciwległych, nie ma szerokości; natomiast szerokość maksymalna, którą planeta osiąga w punktach odległych od węzłów o ćwiartkę obwodu, przybiera bardzo różne wartości. Nachylenie osi i deferentów jakby zawieszonych w owych węzłach jest największe wtedy, gdy Ziemia znajduje się najbliżej planety, to znaczy podczas jej wieczornego wschodu. W tych momentach oś deferentu Saturna nachyla się pod kątem 2 i dwóch trzecich stopnia, Jowisza - dwóch stopni bez jednej trzeciej. Marsa zaś - jednego i pięciu szóstych. Natomiast podczas zachodu wieczornego i wschodu porannego, kiedy Ziemia oddala się od planety najbardziej, tego rodzaju nachylenie u Saturna i Jowisza zmniejsza się o pięć dwunastych stopnia, u Marsa zaś o jeden i dwie trzecie. Ta różnica daje się zauważyć przede wszystkim przy największych szerokościach i jest tym mniejsza, im bliżej węzła znajduje się planeta, wzrasta więc i maleje razem z szerokością.
Ponadto ruch Ziemi po wielkim kole powoduje zmniejszanie się obserwowanych szerokości. Zależnie od tego, czy znajduje się ona blisko, czy daleko, kąty obserwowanej szerokości zwiększają się i zmniejszają zgodnie z zasadami matematyki. Ten ruch libracji odbywa się wprawdzie po linii prostej, można go jednak wyprowadzić z ruchu dwóch sfer. Sfery te są współśrodkowe, ale jedna wodzi nachylone bieguny drugiej. Dolna, wykonując obroty w kie- runku przeciwnym niż górna z prędkością dwa razy większą, obraca bieguny sfery unoszącej epicykle. Bieguny te nachylone są pod tym samym kątem do biegunów sfery wyższej, co jej bieguny do biegunów sfery najwyższej. Tyle o Saturnie, Jowiszu i Marsie oraz ich sferach otaczających Ziemię.
PLANETY DOLNE
O Wenus
Należy jeszcze omówić ruch planet, które zamyka w sobie wielkie koło, to znaczy - ruchy Wenus i Merkurego. Wenus ma podobny system ruchów jak planety górne, lecz wzajemny stosunek tych ruchów jest inny. Deferent, jak już powiedziano przedtem, dokonuje jednego obrotu w ciągu dziewięciu miesięcy. W tym samym czasie pełny obrót wykonuje jego epicykl. W wyniku tego złożonego ruchu mniejszy epicykl w każde miejsce firmamentu wraca ustawiony w ten sam sposób, a jego górna absyda zajmuje punkt, w którym, jak powiedzieliśmy, Słońce zawraca. Czas obrotu jego mniejszego epicykla nie równa się czasowi obrotu deferentu i epicykla większego, nie jest też równy okresowi obrotu wielkiego koła; w czasie, w którym koło to obróci się jeden raz, mniejszy epicykl wykona dwa pełne obroty. Dlatego kiedy Ziemia znajdzie się na średnicy poprowadzonej przez absydę, planeta zajmuje położenie najbliższe środkowi większego epicykla, a najdalej od tego punktu jest wtedy, gdy Ziemia znajduje się w odległości ćwiartki obwodu koła od położenia poprzedniego, to znaczy na średnicy prostopadłej do średnicy przechodzącej przez absydę. W podobny sposób zachowuje się mniejszy epicykl Księżyca względem Słońca. Promień wielkiego koła do promienia deferentu Wenus ma się jak 25 do 18, większy epicykl równy jest trzem czwartym, mniejszy zaś - jednej czwartej.
Wenus również zdaje się czasem zawracać, zwłaszcza zaś wtedy, kiedy jest najbliżej Ziemi. Dzieje się to w podobny sposób jak w ruchu planet górnych, lecz na odwrót. Cofanie się planet górnych jest bowiem skutkiem szybszego ruchu Ziemi, w wypadku Wenus - skutkiem wolniejszego. Planety górne wielkie koło zamykają w sobie, Wenus zaś znajduje się wewnątrz niego. Dlatego nie jest nigdy w opozycji do Słońca (gdyż Ziemia nie może się znaleźć między nimi), lecz zmienia ona swój ruch na przeciwny w stałych od niego odległościach, określonych przez styczne wychodzące ze środka Ziemi i nie przekraczających nigdy 48 stopni dla naszego wzroku. Tak wygląda cały ruch Wenus w długości.
Również w szerokości zmienia swe położenie, co następuje z dwóch przyczyn. Oś jej deferentu nachyla się pod kątem dwóch i pół stopnia, a węzeł, z którego podąża na północ, znajduje się w jej absydzie. Przesunięcie, które powstaje wskutek tego nachylenia, wydaje się nam dwojakie, chociaż samo w sobie jest ono jednakowe. Kiedy bowiem Ziemia znajduje się w jednym z dwóch węzłów Wenus, przesunięcie to spostrzegamy jako dokonujące się w górę, kiedy zaś jest w węźle przeciwległym, wydaje się nam, że odbywa się ono w dół. Przesunięcia te noszą nazwę refleksji. Właściwe Wenus nachylenia deferentu stają się widoczne w momentach, gdy Ziemię od węzłów dzieli odległość ćwiartki koła, i nazywają się deklinacjami. W pozostałych pozycjach Ziemi obie szerokości mieszają się i łączą ze sobą i raz przeważa jedna, raz druga; w zależności od tego, czy w danej chwili są podobne, czy różne, zwiększają się wzajemnie albo zmniejszają. Natomiast nachylenie osi podlega libracji przemieszczającej się i zawieszonej nie w węzłach, jak w wypadku planet górnych, lecz w pewnych innych punktach, które są ruchome i których obiegi w odniesieniu do planety dokonują się w ciągu roku. Dlatego, kiedy Ziemia znajduje się naprzeciw absydy Wenus, libracja jest największa, niezależnie od tego, przez jaki punkt swego deferentu przechodzi sama planeta. Toteż jeżeli planeta znajduje się w absydzie albo w punkcie jej przeciwległym, nie będzie zupełnie pozbawiona szerokości, chociaż będzie wtedy w węzłach. Dalej zaś libracja będzie się zmniejszać tak długo, aż Ziemia odsunie się od wspomnianego miejsca o ćwiartkę obwodu koła, a punkt największej jej dewiacji oddali się wskutek podobieństwa ruchów na tę samą odległość, tak że dewiacja ta nie zostawi najmniejszego nawet śladu. Następnie dewiacja będzie się zmniejszała w dalszym ciągu, a ów punkt początkowy będzie się odchylał z północy na południe i coraz bardziej oddalał od planety zgodnie z odległością Ziemi od absydy. Planeta znajdzie się wskutek tego w tej części obwodu, która przedtem była południową, a teraz na zasadzie przeciwstawienia stanie się północną, i będzie tam tak długo, aż zakończywszy cykl libracji osiągnie jej górną granicę. Wtedy dewiacja osiągnie znowu wartość największą i będzie taka sama, jak była na początku. W ten sam sposób przebiega również przez pozostałą połowę obwodu. Dlatego szerokość ta, zwana powszechnie dewiacją, nigdy nie staje się południową. Zjawiska te, jak się wydaje, należy także tutaj wyprowadzić z ruchu dwóch sfer współśrodkowych o nachylonych osiach, podobnie jak to czyniliśmy mówiąc o sferach położonych wyżej.
O Merkurym
Lecz ze wszystkich ruchów na niebie najdziwniejszy jest bieg Merkurego, który przemierza drogi niemal niepoznawalne i wskutek tego niełatwo może być badany. Dodatkową trudność stwarza fakt, że najczęściej biegnie niewidoczny w promieniach Słońca i bardzo niewiele jest dni, w których go można oglądać. Lecz i on zostanie zbadany, jeśli się tylko w badaniu okaże większą przenikliwość. Podobnie jak dla Wenus, stosowane są dlań dwa epicykle krążące po swym deferencie. Większy epicykl dokonuje obrotu w tym samym czasie co deferent, podobnie jak to było u Wenus, a jego absyda znajduje się czternaście i pół stopnia za Kłosem Panny. Mniejszy natomiast porusza się w kierunku przeciwnym niż tamten i obraca się z szybkością dwa razy większą niż Ziemia. Skutkiem tego, ilekroć Ziemia znajduje się ponad jego absydą albo po stronie przeciwnej, planetę dzieli największa odległość od środka większego epicykla, natomiast w momencie, gdy od owych punktów oddali się o ćwiartkę obwodu koła, odległość ta jest najmniejsza. Jak już powiedzieliśmy, deferent Merkurego dokonuje obrotu w ciągu trzech miesięcy, to znaczy 88 dni. Jego promień składa się z dziewięciu i dwóch piątych takich części, na jakich 25 podzieliliśmy promień wielkiego koła. Promień pierwszego epicykla równy jest jednej takiej części i 41 jej minutom, promień drugiego stanowi jedną trzecią promienia pierwszego, czyli ma prawie 34 minuty. Lecz tutaj, inaczej niż w wypadku pozostałych planet, ten zbiór kół nie wystarcza. Kiedy bowiem Ziemia przechodzi przez wspomniane położenia względem absydy, wtedy wydaje się, że planeta odbywa swój obieg po drodze o wiele mniejszej, niż na to wskazuje wyżej opisany system kół, kiedy natomiast znajduje się w miejscach oddalonych od tych położeń o ćwiartkę koła, wydaje się znowu, że odległość ta jest o wiele większa. Ponieważ nie zauważa się, by z tej przyczyny powstała jakaś inna nieprawidłowość w długości, wydaje się słuszne przypuszczenie, że dzieje się to wskutek jakiegoś przybliżania się planety do środka deferentu i oddalania się od tego punktu po linii prostej. Można to wytłumaczyć ruchem dwóch małych kółek o osiach równoległych do osi wielkiego koła. Środek większego epicykla czy też całego systemu oddalony jest o tę samą odległość od środka unoszącego go kółka pośredniego, co środek tegoż kółka od środka kółka zewnętrznego. Zostało obliczone, że odległość ta wynosi 14 i pół minuty takiej spośród 25 części, jakimi określaliśmy wielkość i układ wszystkich kół. Kółko zewnętrzne w ciągu roku zwrotnikowego wykonuje dwa obroty, wewnętrzne zaś poruszając się w kierunku przeciwnym obraca się w tym czasie cztery razy. Tym złożonym ruchem środek większego epicykla przesuwa się po linii prostej tak, jak wyjaśniliśmy objaśniając librację w szerokości. W ten więc sposób, przy wspomnianych pozycjach Ziemi względem absydy, odległość środka epicykla od środka wielkiego koła jest największa, natomiast najmniejsza wtedy, gdy Ziemia oddalona jest od tych pozycji o ćwiartkę koła. Natomiast, gdy Ziemia jest w punktach pośrednich, to znaczy w odległości 45 stopni od tych miejsc, wtedy środek większego epicykla pokrywa się ze środkiem zewnętrznego kółka. Wielkość tego przybliżenia i oddalenia równa się 29 minutom jednej ze wspomnianych poprzednio części. W ten sposób odbywa się ruch Merkurego w długości.
W szerokości porusza się tak samo jak Wenus, lecz zawsze po przeciwnej stronie. Mianowicie, gdzie Wenus jest w szerokości północnej, tam on - w południowej. Jego deferent jest nachylony do ekliptyki pod kątem siedmiu stopni. Przesunięcie, które również jest zawsze południowe, nigdy nie przekracza trzech czwartych stopnia. Resztę, by nie powtarzać ciągle tego samego, pominiemy odsyłając do tego, co o szerokości powiedziano przy omawianiu Wenus.
Tak tedy mamy razem siedem kół, po których biegnie Merkury. Wenus porusza się po pięciu, Ziemia – po trzech, Księżyc wokół niej – po czterech, Mars wreszcie, Jowisz i Saturn mają ich po pięć. Wystarczą więc w sumie 34 koła dla wytłumaczenia całej budowy świata i całego korowodu planet.
Przekład Jerzego Drewnowskiego
Źródło:
- Mikołaj Kopernik, Pisma pomniejsze, Warszawa 2007.
NICOLAI COPERNICI DE HYPOTHESIBUS MOTUUM CAELESTIUM A SE CONSTITUTISCOMMENTARIOLUS
(PARS INTRODUCTIVA GENERALIS)
Multitudinem orbium caelestium maiores nostros eam maxime ob causam posuisse video, vt apparentem in sideribus motum sub regularitate saluarent. Valde enim absurdum videbatur caeleste corpus in absolutissima rotunditate non semper aeque moueri. Fieri autem posse animaduerterant, vt et compositione atque concursu motuum regularium diuersimode ad aliquem situm moueri quippiam videretur.
Id quidem Calippus et Eudoxus per concentricos circulos deducere laborantes non potuerunt et his omnium in motu sidereo reddere rationem, non solum eorum, quae circa reuolutiones siderum videntur, verum etiam, quod sidera modo scandere in sublime, modo descendere nobis videntur, quod concentricitas minime sustinet. Itaque potiore visa est sententia per eccentricos et epicyclos id agi, in qua demum maxima pars sapientium conuenit. Attamen quae a Ptolemaeo et plerisque alijs passim de his prodita fuere, quamquam ad numerum responderent, non paruam quoque videbantur habere dubitationem. Non enim sufficiebant, nisi etiam aequantes quosdam circulos imaginarentur, quibus apparebat neque in orbe suo deferente, neque in centro proprio aequali semper velocitate sidus moueri. Quapropter non satis absoluta videbatur huiusmodi speculatio neque rationi satis concinna.
Igitur cum haec animaduertissem ego, saepe cogitabam, si forte rationabilior modus circulorum inueniri possit, e quibus omnis apparens diuersitas dependeret, omnibus in se ipsis aequaliter motis, quemadmodum ratio absoluti motus poscit. Rem sane difficilem aggresso ac paene inexplicabilem obtulit se tandem, quomodo id paucioribus ac multo conuenientioribus orbibus, quam olim sit proditum, fieri possit, si nobis aliquae petitiones, quas axiomata vocant, concedantur: quae hoc ordine sequuntur.
Prima petitio
Omnium orbium caelestium seu sphaerarum vnum centrum non esse.
Secunda petitio
Centrum Terrae non esse centrum mundi, sed tantum grauitatis et orbis lunaris.
Tertia petitio
Omnes orbes ambire Solem tamquam in medio omnium existentem, ideoque circa Solem esse centrum mundi.
Quarta petitio
Minorem esse comparationem distantiarum Solis et Terrae ad altitudinem firmamenti, quam semidimetientis Terrae ad distantiam Solis, adeo vt sit ad summitatem firmamenti insensibilis.
Quinta petitio
Quicquid ex motu apparet in firmamento, non esse ex parte ipsius sed Terrae. Terra igitur cum proximis elementis motu diurno tota conuertitur in polis suis inuariabilibus firmamento immobili permanente ac vltimo caelo.
Sexta petitio
Quidquid nobis ex motibus circa Solem apparet, non esse occasione ipsius, sed Telluris et nostri orbis, cum quo circumuoluimur ceu aliquod aliud sidus, sicque Terram pluribus motibus ferri.
Septima petitio
Quod apparet in erraticis retrocessio ac progressus, non esse ex parte ipsarum, sed Telluris. Huius igitur solus motus tot apparentibus in caelo diuersitatibus sufficit.
His igitur sic praemissis conabor breuiter ostendere, quam ordinate aequalitas motuum seruari possit. Hic autem brevitatis causa mathematicas demonstrationes omittendas arbitratus sum, maiori volumini destinatas. Quantitates tamen semidiametrorum orbium in circulorum ipsorum explanatione hic ponentur, e quibus mathematicae artis non ignarus facile percipiet, quam optime numeris et obseruationibus talis circulorum compositio conueniat.
Proinde ne quis temere mobilitatem Telluris asseuerasse cum Pythagoricis nos arbitretur, magnum quoque et hic argumentum accipiet in circulorum declaratione.
Etenim quibus physiologi stabilitatem eius astruere potissime conantur, apparentijs plerumque innituntur: quae omnia hic inprimis corruunt, cum etiam praeter apparentiam versemur eandem.
De ordine orbium
Orbes celestes hoc ordine se complectuntur. Summus est stellarum fixarum immobilis et omnia continens et locans, sub eo Saturnius, quem sequitur Jouius, hunc Martius. Subest huic orbis, in quo nos circumferimur, deinde Venereus, vltimus Mercurialis. Orbis autem Lunae circa centrum Terrae vertitur, et cum eo ceu epicyclus defertur. Eodem quoque ordine alius alium reuolutionis velocitate superat, secundum quod maiora minoraue circulorum spatia emetiuntur. Sic quidem Saturnus anno trigesimo, Iupiter duodecimo, Mars biennio, Tellus annua reuolutione restituitur, Venus nono mense, Mercurius tertio reuolutionem peragit.
DE MOTIBUS QUI CIRCA SOLEM APPARENT
Terra triplici motu circumfertur. Vno quidem in orbe magno, quo Solem ambiens secundum signorum successionem anno reuoluitur, in temporibus aequalibus semper aequales arcus describens: cuius quidem centrum a centro Solis vigesima quinta parte semidiametri sui distat. Cum igitur supponatur semidiametrum huius orbis ad altitudinem firmamenti imperceptibilem habere quantitatem, consequens est, vt hoc motu Sol circumferri videatur, perinde ac si Terra in centro mundi subiaceat, cum tamen id non Solis sed Terrae potius motione contingit: vt exempli causa, dum haec sit sub Capricorno, Sol e directo per diametrum in Cancro cernatur, et sic deinceps. Videbitur etiam Sol eo motu inaequaliter moueri secundum distantiam eius a centro orbis, vt iam dictum est: ex quo maxima diuersitas duobus gradibus et sextante vnius contingit. Declinat autem ab ipso centro Sol ad punctum firmamenti, quod distat a stella lucida, quae est in capite Gemelii splendidior, gradibus fere 10 versus occidentem inuariabiliter. Tunc igitur Sol in summa eius altitudine cernitur quando Terra in loco huic opposito versatur, centro orbis inter eos mediante, et per hunc quidem orbem non Terra solum, sed quicquid simul cum orbe lunari comprehensum est, circumducitur.
Allius Telluris motus est quotidianae reuolutionis et hic sibi maxime proprius in polis suis secundum ordinem signorum hoc est ad orientem labilis, per quem totus mundus praecipiti voragine circumagi videtur. Sic quidem Terra cum circumfluis aqua et vicino aere voluitur.
Tertius est motus declinationis. Axis enim quotidianae reuolutionis non aeque distat axi magni orbis, sed obliquatur secundum circumferentiae partem, nostro quidem saeculo 23 gradibus et medio fere. Igitur centro Terrae in superficie eclipticae semper manente hoc est in circumferentia circuli magni orbis, poli eius circumaguntur circulos vtrobique paruos describentes in centris ab axe orbis magni aequidistantibus. Et hic quoque motus annuas fere complet reuolutiones et cum orbe magno paene compares. At vero axis magni orbis ad firmamentum immutabilem seruat compositionem ad eos quos vocant eclipticae polos. Motus item declinationis cum motu orbis complexus polis quotidianae reuolutionis ad eadem caeli momenta semper retineret, si paribus omnino reuolutionibus cum illo constaret. Nunc longo temporis tractu deprehensum est talem Telluris positionem ad faciem firmamenti mutari, propter quod ipsum firmamentum aliquibus motibus ferri plerisque visum est, lege nondum satis deprehensa. Posse autem haec omnia fieri mutabilitate Telluris minus mirum est. Quibus autem poli inhaereant, ad me non attinet dicere. Video equidem in vilioribus rebus, quod virgula ferrea magnete attrita in vnum semper mundi situm nitatur. Potior tamen sententia visa est, secundum orbem aliquem fieri, ad cuius notum ipsi poli moueantur, quem procul dubio sub Luna esse oportebit.
Quod aequalitas motum non ad aequinoctia, sed ad stellas fixas referatur.
Cum igitur aequinoctialia puncta caeterique mundi cardines plurimum commutentur, falli eum necesse est. Quicunque ab his aequalitatem annuae reuolutionis deducere conatur, quae etiam sub diuersis aetatibus multis experimentis obseruationum diuersa reperta est. Hanc Hipparchus 365 diebus cum quadrante vnius diei, Albategni vero Chaldaeus reperit talem annum ex 365 diebus, 5 horis, 46 minutis, hoc est 13 minutis et 3 quintis Ptolemaico breuiorem. Rursus autem Hispalensis hunc longiorem vigesima parte vnius horae, siquidem ex 365 diebus, 5 horis et 49 minutis annum vertentem constituit.
Ne autem diuersitas ex obseruationum errore processisse videatur si quis singula accuratius animaduertet, inueniet eam cum mutabilitate aequinoctialium punctorum semper correspondisse. Dum enim ipsi mundi cardines in centenis annis vno gradu mutabantur, quemadmodum Ptolemaei aeuo repertum est, erat tunc anni quantitas quae ab ipso Ptolemaeo tradita est. Quando autem subsequentibus saeculis potiori mutabilitate mouerentur motibus inferioribus obuiantes, tanto breuior annus factus est, quanto translatio cardinum esset maior. Nam occursu velociori breuiori tempore anuum excipiebant motum. Rectius igitur agit, quicunque annuam aequalitatem ad stellas fixas referet. Quemadmodum circa Virgini Spicam fecimus inuenimusque annum 365 dierum et 6 horarum et sextantis fere vnius horae semper fuisse, qualis etiam in Aegyptiaca antiquitate reperitur. Eadem ratio in alijs etiam motibus siderum habenda est, quod absides eorum et statae sub firmamento motuum leges docent ac caelum ipsum veraci testimonio.
DE LUNA
Luna praeter annalem, vt dictum est, circuitum quatuor motibus videtur peruagari. Nam in orbe suo deferente circa telluris centrum secundum ordinem signorum menstruas complet reuolutiones. Is vero defert, quem vocant epicyclum primae diuersitatis siue augmenti, nos vero primum siue maiorem et qui epicyclum alterum sibi inhaerentem in superiore quidem portione contra motum orbis reflexus paulo tardiore quam menstruo tempore deducit. In hoc demum Luna pendens binas in mense reuolutiones contra motum illius perficit, vt, quandocumque centrum epicycli maioris contingit, lineam a centro orbis magni transeuntem per centrum Terrae, quam diametrum magni orbis vocamus, tunc Luna sit ad centrum maioris epicycli proxima, quod quidem circa nouam et plenam Lunam accidit, at econtra in quadraturis mediantibus ijsdem remotissima. Quantitas autem semidiametri epicycli maioris continet decimam partem de semidiametro orbis sui deferentis cum decima octava vnius particula, minoris vero epicycli semidiametrum quinquies dempta vna quarta ipsius.
Per haec igitur Luna modo concita modo tarda descendens, quoque et ascendens videtur, et primae quidem diversitati, dupliciter variationem motus epicycli minoris ingerit: Lunam enim in circumferentia maioris ab aequalitate distrahit, cuius quidem in hoc maxima diuersitas 12 gradus et quadrantem colligit de circumferentia ipsa quantitatis seu diametric respondentis; eam quoque a centro maioris modo distrahit modo appellit secundum semidiametri magnitudinem. Cum igitur propter hoc circa centrum maioris epicycli inaequales circulorum ambitus Luna describat; contingit primam diuersitatem multipliciter variari. Hinc est quod circa coniunctiones et obiectiones ad Solem maxima huiusmodi diuersitas 4 gradus et 56 minuta non exedat in quadraturis autem ad 7 gradus et 36 minuta extendatur. Qui vero per eccentricum circulum fieri hoc arbitrantur, praeter ineptam in ipso circulo motus inaequalitatem in duos inciderunt manifestos errores. Consequens enim est cum mathematica ratione, quod Luna in quadraturis, dum infima parte epicycli dependet, quadruplo fere maior appareat (si modo tota luceret) quam noua et plena nisi argumentum et diminutionem corporis sui magis temerarie quispiam asserit. Sic quoque diuersitatem aspectus facit propter notabilem terrae magnitudinem ad distantiam eius circa quadraturas plurimum augeri. Si quis autem diligentius perscrutetur, parum valde vtrumque distare comperiet in quadraturis ab his quae interlunio plenaque Luna contingunt, et proinde veriorem hanc speculationem nostram haud facile dubitabit.
His vero tribus motibus longitudinum Luna circumit puncta latitudinis motus, axes quidem epicyclorum aequidistant axi orbis propter quod nullam ab eo agressionem facit. Sed hic orbis axem suum decliuem habet axi magni orbis siue eclipticae, quapropter Lunam a superficie eclipticae digredi facit. Declinat igitur secundum quantitatem anguli, cui de circumferentia circuli 5 gradus supratenduntur, cuius poli circumferentur in aequidistantia axis eclipticae, propemodum sicut in declinatione dictum est: sed hic contra signorum ordinem et longo tardiore motu, vt ad vnam reuolutionem decimum nonum annum expectet. Et hoc in orbe quidem eminentiore fieri plerisque videtur, cui poli inhaerentes ad hunc modum ferantur. Talem igitur videtur habere Luna motuum fabricam.
DE TRIBUS SUPERIORIBUS: SATURNO, IOUE ET MARTE
Saturnus, lupiter et Mars similem habent motuum rationem, siquidem orbes eorum annalem illum magnum penitus includentes in centro communi ipsius magni orbis ad ordinem signorum voluuntur. Sed orbis quidem Saturnius trigesimo anno reducitur, Iouianus duodecimo, Martius autem vigesimo nono mense, perinde ac si tales reuolutiones magnitudo orbium remoraretur. Nam semidiametro magni orbis ex 25 partibus constituto, semidiameter orbis Martij 38 partes obtinet, Iouis 130 et vnius particulae quincuncem, Saturni 230 et sextantem vnius. Dico autem semidiametrum a centro orbis ad centrum primi epicycli distantiam. Habet enim quisque duos epicyclos, quorum alter alterum defert, propemodum sicut in Luna dictum est, sed lege diuersa. Primus enim epicyclus contra motum orbis reflexus pares facit cum eo reuolutiones, altero vero obuians primi motum reuolutionibus duplicatis circumagit sidus, adeo vt quandocunque sit in summa a centro orbis distantia vel rursus in maxima vicinitate, tunc sidus sit centro epicycli quam proximum, in quadrantibus autem mediantibus remotissimum. Igitur ex talium motuum compositione orbis et epicyclorum et reuolutionum paritate contingit, vt huiusmodi elongationes et accessiones maxime statas sibi sub firmamento sedes obtineant, ac deinceps certas vbique obseruant motuum conditiones. Itaque absides suas inuariabiles habent, Saturnus quidem circa stellam quae super cubitum esse dicitur Sagittatoris, Iupiter gradibus 8 post stellam quae extremitas caudae Leonis appellatur, Mars vero gradibus 6 et medio ante Cor Leonis.
Magnitudines autem epicyclorum hae sunt. In Saturno quidem primi semidiameter constat ex partibus 19 et 41 minutis, qualium semidiameter orbis magni ex 25 supponebatur; secundus autem epicyclus partium 6 et minutorum 34 semidiametrum habet. Sic quoque in Ioue primus partium 10 et minutorum 6, secundus partium 3 et minutorum 22 semidiametros continerent. In Marte autem primus partium 5 minutorum 34, secundus partis 1 minutorum 51. Sic igitur vbique ad primum semidiameter triplo maior est secundo.
Hanc autem diuersitatem quam epicyclorum motus inducit super motum orbis, primam appelare placuit, quae vbique sub firmamento certos, vt dictum est, obseruat limites. Alia siquidem est diuersitas, secundum quam sidus interdum regredi, saepe etiam subsistere cernitur, quae non ex motu sideris contingit, sed Telluris in orbe magno aspectum variantis. Haec enim motum sideris velocitate superans radio visuali ad firmamenti aspectum obuiante motum sideris vincit. Quod tunc maxime fit, quando proxima fuerit sideri Terra, dum videlicet inter Solem et sidus mediat vespertini sideris ortu. Econtrario autem circa vespertinum occasum ortumue matutinum praeuentione antefert visum. Vbi vero visus contra motum aequali cursu obuiat, stare videtur aduersis motibus inuicem se sic perimentibus, quod plerumque circa triquetrum Solis radium contingit. In his autem omnibus tanto maior contingit talis diuersitas, quanto inferiore orbe sidus mouetur, vnde minor in Saturno quam Ioue, et rursus in Marte maxima, secundum proportionem semidiametri magni orbis ad illorum semidiametros. Fit autem tunc vniuscuiusque maxima, quando sidus per radium aspicitur circumferentiam magni orbis contingentem, equidem tria haec sidera nobis pererrant.
In latitudine vero duplicem digressionem faciunt circumferentijs quidem epicyclorum in vna superficie permanentibus, cum orbe suo ab ecliptica declinant secundum axium deflexiones, non sicut in Luna circumducibiles, sed in eundem caeli tractum semper vergentes. Igitur et sectiones circulorum orbis et eclipticae, quas nodos vocant, aeternas in firmamento sedes occupant. Sic quidem Saturnus nodum suum habet, vnde ad septentriones scandere incipit, partibus 8 et media post stellam, quae in capite Geminorum orientalis dicitur; Iupiter ante eam ipsam stellam partibus 4, Mars vero Vergilias antecedentem partibus 6 et medio. In his igitur ac e diametro positis sidus existens nullam habet latitudinem, maximam vero, quae in his in quadraturis contingit, valde diuersam. Nam axium circulorumque inclinatio tanquam nodis illis pensilis instare videtur: tunc equidem maxima fit, quando Tellus sideri proxima est, hoc est in ortu sideris vespertino. Tunc enim in Saturno partibus duabus et besse axis inclinatur, in Ioue partibus 2 dempto triente, in Marte vero parte l et dextante. Econtra autem circa vespertinum occassum ortumque matutinum: plurimum tunc absente Terra Saturno quidem et Ioui quincunce vnius partis minor est huiusmodi inclinatio, Marti vero parte 1 et besse. Sic quidem diuersitas haec in maximis latitudinibus apprime percipitur, ac allicui tanto minor, quanto minus a nodo sidus distat pariter cum latitudine crescens et decrescens.
Accidit etiam motu Telluris in orbe magno latitudines visibiles nobis variari, ita sane propinquitate et distantia visibilis latitudinis angulos augente et minuente, sicut mathematica ratio exposcit, siquidem hic motus librationis secundum lineam rectam contingit. Fieri autem potest, vt ex duobus orbibus huiusmodi motus componatur, qui cum sint concentrici, alter alterius deflexos circumducit polos et inferior contra superiorem duplici velocitate polos orbis epicylos deferentis reuoluat; et hi quoque poli tantam habeant deflexionem a polis orbis mediate superioris, quantum huius a polis supremi orbis. Et haec de Saturno, Ioue et Marte ac orbibus Terram abientibus.
QUAE MAGNI ORBIS AMBITU INCLUDUNTUR
De Venere
Reliquum est eorum speculationem aperire, quae magni orbis ambitu includuntur, hoc est de motibus Veneris et Mercurij. Venus quidem persimilem habet circulorum compaginem qualem illi superiores, sed alia motum obseruantia.
Orbis quidem cum epicyclo suo maiori pares facit reuolutiones nono mense, vt praedictum est, eoque motu composito minorem epicyclum certa ubique habitudine firmamento restituit, summam eius absidem ad punctum, quo Solem vergere diximus, constituens. Minor autem epicyclus, impares cum illis reuolutiones habens, motui orbis magni imparitatem reseruauit. Ad huius quidem reuolutionem duos omnino circuitus perficit, vt, quandocunque Tellus in linea ad absidem diametro porrecta fuerit, sidus tunc centro maioris epicycli proximum sit et in transuerso quadrantum remotissimum simili fere modo, quemadmodum in Luna minor epicyclus Solem respicit, obseruans. Est autem proportio semidiametrorum orbis magni et Veneris sicut 25 ad 18, et maior epicyclus dodrantem suscipit vnius particulae, minor vero quadrantem.
Retrocedere quandoque et haec cernitur, tunc maxime quando sidus Terrae proximum est, simili quodammodo ratione vt in superioribus, sed conuersa. In illis enim accidit motu Terrae superante, hic autem superato, ac illic orbe Telluris contento, hic vero continente. Quapropter nec unquam Soli opponitur, cum Tellus intermediari non possit, sed ex certis a Sole distantijs, quae fiunt in contactibus circumferentiae lineis a centro Telluris prodeuntibus, vtrobique reuertitur, 48 gradus nunquam excedens ad nostrum aspectum. Et haec est Venerei motus summa, quo in longitudinem circumducitur.
Latitudinem quoque duplici causa scandit. Habet enim et haec axem orbis inclinatum quantitate anguli graduum duorum cum semissi. Et nodum suum, vnde septentriones petit, in abside sua habet. Digressio autem, quae ex tali inclinatione procedit, quamquam eadem in se ipsa sit, duplex ostenditur. Nam in alterutro nodorum Veneris incidente Terra transversis sursum et deorsum aspiciuntur: has reflexiones vocant; naturales apparent orbis obliquitates, et has vocant declinationes, eadem vero in quadrantibus. Caeteris autem locis ambae latitudines permixtae confunduntur ac alia aliam superans vincit ac similitudine ac dissimilitudine mutuo se augent et perimunt. Haec vero axis inclinatio est: habet librationem mobilem, non autem sicut in superioribus illis ad nodos pendentem, sed in alijs quibusdam volubilibus punctis, quae reuolutiones suas ad sidus annuas faciunt, vnde, quandocunque Tellus contra absidem Veneris steterit, maxima tunc fit librationis inflexio et haec in ipso sidere, in quacumque tunc parte sui orbis fuerit. Quapropter si tunc sidus in abside sit vel ei diametraliter opposito, latitudine non penitus carebit, tametsi in nodis tunc versetur. Hinc vero decrescente hac inflexione quoadusque Tellus per quadrantem circuli dicto loco amoueatur et similitudine motuum maximae illius deuiationis punctus a sidere tantundem destiterit, nullum prorsus huiusce deuiationis vestigium vsquam reperitur. Et deinceps deuiationem libramento continuato et illo principio a septentrionibus ad austrum declinante ac identidem a sidere sese elongante secundum Telluris ab abside remotionem sidus ad eam perducitur partem, quae prius australis fuerat, nunc autem oppositionis lege septentrionalis facta, donec iterum ad summam perueniat librationis circulo peracto, vbi rursum maxima fit deuiatio et primae similis et aequalis. Sic demum pari modo per reliquum semi circulum pergit. Quapropter nunquam fit meridiana haec latitudo, quam plerumque deuiationem vocant. Et haec duobus orbibus fieri concentricis et axibus obliquis, sicut in superioribus orbibus dieebamus, hic quoque consentaneum esse videtur.
De Mercurio
Sed omnium in caelo mirabilissimus est Mercurij cursus, qui paene imperuestigabiles permeat vias, vti perscrutari non facile queat. Addit praeterea difficultatem, quod sub radijs Solis inuisibiles plerumque meatus occupat et paucis admodum diebus visibilem se exhibet: attamen comprebendetur et ipse, modo altiori ingenio quispiam incumbat. Conuenient et huic epicycli duo, vt in Venere, in orbe suo reuolubiles. Nam maior epicyclus cum orbe suo pariter facit reuolutiones, vt illic, absidis eius sedem gradibus 14 et medio post Virginis Spicam constituens, Minor autem epicyclus contraria illius lege duplici vero reuolutione relfectitur, vt in omni situ Telluris, quo absidem huius superauerit vel ex aduerso respicit, sidus a centro maioris epicycli remotissimum sit atque in quadrantibus proximum. Et huius quidem orbem tertio mense diximus reuerti, hoc est 88 diebus, cuius semidimetiens partes capit 9 et duas quintas vnius partis, quarum semidiametrum magni orbis 25 posuimus. Ex his autem primus epicyclus accipit 1 et 41 minuta, secundus autem tertiam eius partem, hoc est minuta 34 fere. Sed is quidem circulorum concursus hic non sufficit vt in caeteris. Terra siquidem in supradictis absidis respectibus permeante, longo minori apparet ambitu sidus moueri, quam ratio circulorum iam dicta sustinet, et rursus in quadraturis longe etiam maiore. Cum vero nullam aliam in longitudine diuersitatem ex hoc fieri parcipiatur, consentaneum est per accessum quendam et recessum a centro orbis secundum lineam rectam contingere. Quod quidem fieri oportet duobus orbiculis circumdatis habentibus axes aequidistantes axi orbis, dum centrum epicycli maioris siue totius illius asse tantum distat a centro orbiculi immediate continentis, quantum centrum huius a centro extremi. Id quidem repertum est minutis 14 et medio vnius partis de 25, quibus omnium contextum mensi sumus: quodque motus extremi orbiculi binas in anno vertente reuolutiones faciat, interior autem motu reflexo duplo recursu quater interim reuertatur. Perferuntur enim hoc motu composito centro maioris epicycli secundum lineam rectam, quemadmodum circa latitudines libratas diximus. Sic igitur in memoratis ad absidem Telluris sitibus centrum epicycli maioris centro orbis proximum est, in quadraturis autem remotissimum. In locis autem mediantibus, hoc est 45 gradus ab his, centrum maioris epicycli centro exterioris orbiculi se applicat amboque in vnum concurrunt. Quantitas autem huiusce recessus et accessus constat minutis 29 vnius praedictarum partium. Et hactenus motus Mercurij longitudinalis sic se habet.
Latitudinem vero haud secus facit quam Venus, sed tractu semper contrario. Vbi enim illa septentrionalis fit, hic austros petit. Declinat autem orbis eius ab ecliptica quantitate anguli partium 7. Deuiatio autem hic quoque semper australis dodrantem vnius gradus nunquam excedit. Caeterum quae circa latitudinem Veneris dicta sunt, hic quoque commemorasse conuenit, ne eadem saepe repetantur.
Sicque septem omnino circulis Mercurius currit, Venus quinque, Tellus tribus et circa eam Luna quatuor. Mars demum, Iupiter et Saturnus singuli quinque. Sic igitur in vniuersum 34 circuli sufficiunt, quibus tota mundi fabrica totaque siderum chorea explicata sit.
Źródło:
- Kopernik Mikołaj, Pisma pomniejsze, Warszawa 2007.
 Polski (PL)
Polski (PL)  English (United Kingdom)
English (United Kingdom)